A Statistical Study of American Men of Science
II. The Measurement of Scientific Merit
James McKeen Cattell
MANY of the problems that the writer had in view in the present research might be solved by the study of any group of a thousand American men of science, so long as they had been objectively selected. The objective selection of a group sufficiently large for statistical treatment is, however, essential. As cases can be quoted to illustrate the cure of nearly every disease by almost any medicine, so examples can be given in support of any psychological or sociological theory. The method of anecdote, as used by Lombroso, may be readable literature, but it is not science. A thousand names might have been selected by lot from all the scientific men of the country, assuming a list to have been available, but a group of the thousand leading men of science arranged in the order of merit has certain advantages. Information in regard to them can be better obtained than in the case of those who are more obscure. Correlations can be determined between degrees of scientific merit and various conditions. The comparison with a similar group selected ten or twenty years hence, or with a similar group of British, French or German men of science, would give interesting results. The list itself, if printed after an interval of twenty years, would be a historical document of value. Lastly, the data can be so used as to carry quantitative methods a little way into a region that has hitherto been outside the range of exact science. It is the last problem that I wish to take up in this paper.
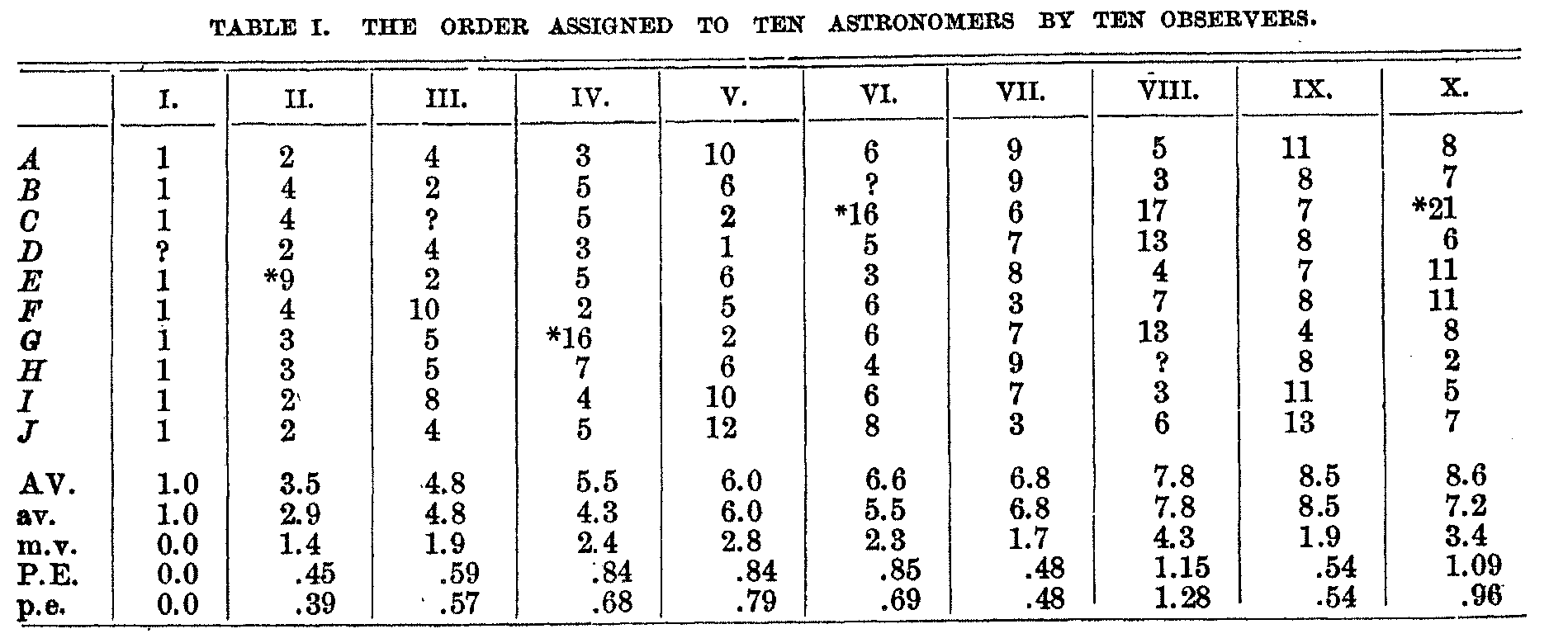
It will be remembered that we have in each science the workers in that science arranged in the supposed order of merit by ten competent judges, who made their arrangements independently. If the ten arrangements agreed exactly, we should have complete confidence in the result, except in so far as it was affected by systematic or constant errors. If there were no agreement at all, the futility of any attempt to estimate scientific merit would be made clear. The conditions are naturally intermediate. There is a certain amount of agreement and a certain amount of difference of opinion. Thus taking, for example, the ten astronomers —I., II., III., etc.—whose average positions were the highest, the order given to them by each of the ten observers, A, B, C, etc., is as shown in the table:
( 700)
Here we find complete agreement that I. is our leading astronomer. He has been selected as such by nine competent judges from the 160 astronomers of the country.[1] The probability that this is due to chance is entirely negligible. II. stands next in scientific merit. He is placed second by four of the observers, third by two, fourth by three and ninth by one. The conditions are similar to observations in the exact sciences. The average position or grade is 3.5, and the probable error of this position is 0.45, i. e., the chances are even that this grade is correct within one half of a unit. The grade of the astronomer who stands third is 4.8, and that of the astronomer who stands fourth is 5.5. There is consequently one chance in about fifty that II. deserves a grade as low as that of III., and one in about one thousand that he deserves a grade as low as that of IV. The order thus has a high degree of validity, and this has itself been measured. As we go further down the list, the probable errors tend to increase, the order is less certain, and the difference in merit between a man and his neighbor on the list is less. The variations in the sizes of the probable errors are, as a rule, significant. When the error is small the work of the man is such that it can be judged with accuracy; when it is larger it is because the work is more difficult to estimate.
The probable errors depend on the assumption that the individual deviations follow the exponential law, and they do so in sufficient measure for the purposes in view. For those near the top of the list, the distribution of errors is 'skewed' in the negative direction, that is, there are relatively more large negative than positive errors. Thus in the table there are four judgments marked with a star, the deviation of each of which is more than three times the average deviation, and these observations would be omitted by an approximate application of Chauvenet's criterion. If these four observations are omitted, the grades of the ten astronomers are those given in the second line of averages. The omitted judgments are not extremely divergent, barely exceeding the limits set by Chauvenet's criterion, and I do not regard them as invalid. Indeed, I believe that in view of the presence of systematic errors in these estimates the chance that they represent correct values is greater than that assigned by a strict application of the theory of probabilities. But the incidence of an extreme judgment might in special cases do injustice to an individual, and in the order used Chauvenet's criterion has been applied.[2] This means that a compromise has been adopted between the median and the average judgment; but the departure from the average judgment is small, affecting less than one fifth of the individuals and only to a slight degree. The average deviations and probable errors used are those found when all the judgments are included. Two probable errors are given in the table, the first obtained through the error of mean square, the second by taking it as directly proportional to the average deviation. The differences are not significant, and for work of this character I regard it as use-less to calculate the probable errors by the ordinary formula. I have published elsewhere [3] a more technical discussion of the treatment of errors or deviations of this character, and may return to the subject at some subsequent time. The theory of errors commonly applied in the exact sciences is too crude for psychology, and probably for the
( 701) sciences in which it is used. Progress here will be blocked until there are psychologists who are mathematicians or mathematicians who are psychologists.
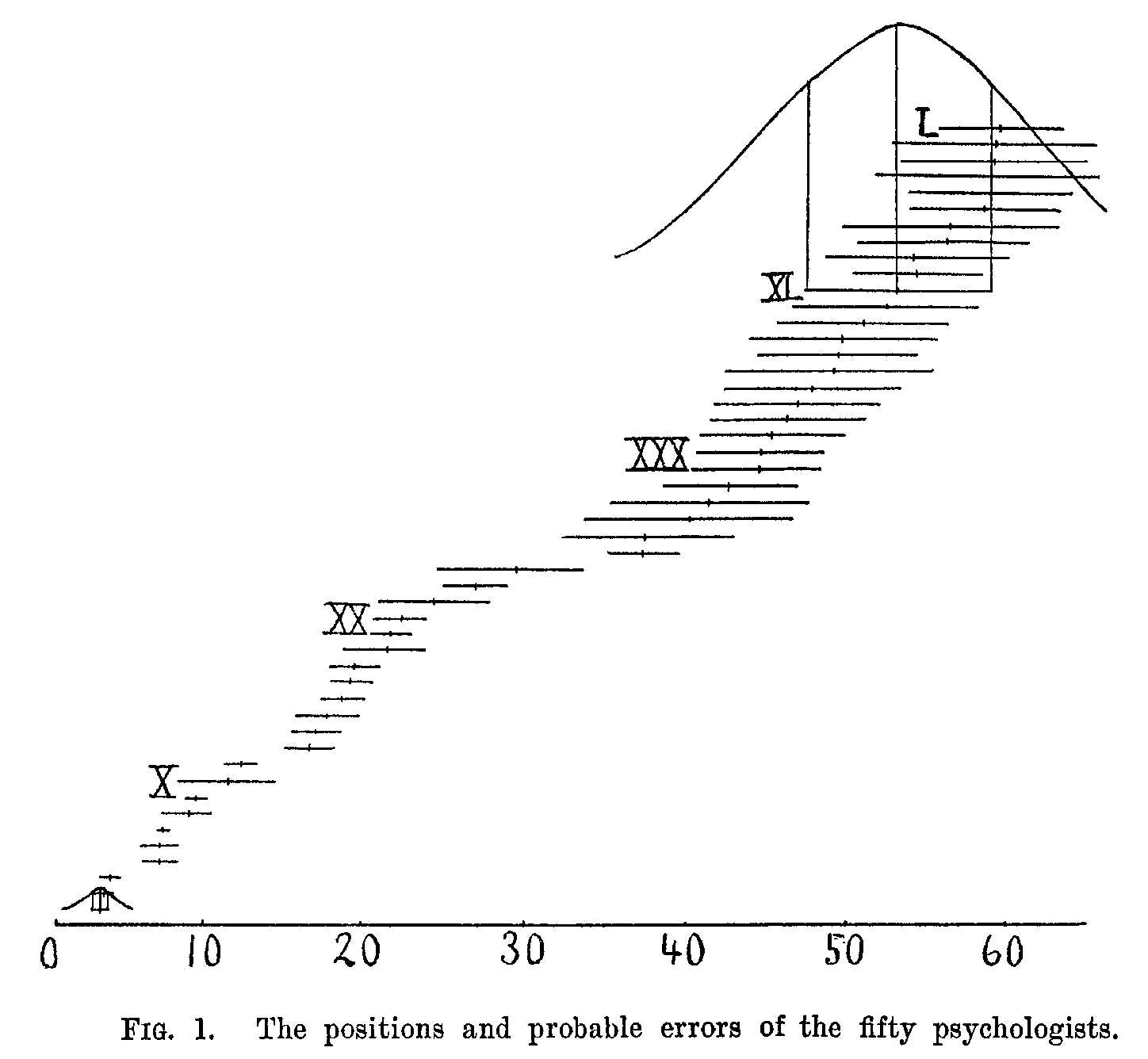
In order to illustrate further the serial distribution and the probable errors, I have made a diagram for the fifty psychologists. The grade of each, no judgments being omitted, is shown by the vertical mark, and the length of the line indicates the probable error or range within which the chances are even that the true position falls. Thus the psychologist who stands first on the list, was, like the astronomer, given this position by the in-dependent judgment of all. The psychologist who stands second has, as shown on the diagram, a position of 3.7 and a probable error of 0.5, i. e., the position 3.7 is the most probable, but the true position is equally likely to be within the short horizontal line, between 3.2 and 4.2, or outside it. It must, however, be remembered that the chances of the true position being far outside the range of this line decrease very rapidly. Over it is roughly drawn the bell-shaped curve of the normal probability integral. The true position is along the base line covered by this curve, and the chances of its being at any given point are proportional to the ordinate or height of the curve above the base line. There is only one chance in about six that the true grade is above 2.7 or below 4.7, and only one chance in about 150 that the true grade is above 1.7 or below 5.7. It will be seen from the diagram that while the positions of the psychologists II., III. and IV. are the most probable, the relative order is not determined with certainty. On the other hand, the chances are some 10,000 to one that each of these psychologists stands below I. and above V.
It is evident that the probable errors in-crease in size as we go down the list. The curve of distribution drawn over No. XL. indicates that the chances are even that the true
( 702) position falls between the grades of XXXIV. and L. and that there is one chance in four that he does not belong among our fifty leading psychologists. The increase in the size of the probable errors is irregular, it being more difficult to assign a position to some men than to others.
It will be noted that the psychologists fall into groups, the first twenty being set off from the next group, though the two groups are bridged over by three cases. At this point also the probable errors become almost suddenly about three times as large. There are altogether about 200 psychologists in the country, and it looks as if the first tenth forms a separate group of leaders. There is a similar, though less marked group of the first twenty astronomers, but these groups seem to be partly accidental. There is, how-ever, as shown below, an inflection point in the curve of distribution after about the first tenth of our scientific men. The first twenty psychologists fall into four distinct groups, and there are groupings in the other sciences. They do not, however, appear to be sufficiently marked to lead us to distinguish species, such as men of genius and men of talent. It is, however, possible that the complicated conditions may ultimately be analyzed so as to give such groups.
The probable errors not only tell the accuracy with which the psychologists can be arranged in the order of merit, but they also measure the differences between them. This, indeed, I regard as the most important result of this paper, as science is advanced chiefly by the extension of quantitative methods, and it might not have been foreseen that it would be possible to measure degrees of scientific merit. Our data are concerned with the recognition of scientific performance, not with abstract ability, if such a thing is conceivable. Merit is in performance, not in non-performance, and expert judgment is the best, and in the last resort the only, criterion of performance.
The difference in scientific merit between any two of the psychologists whose positions and probable errors are shown in the chart is directly as the distance between them and inversely as their probable errors. If two of them are close together on the scale, and if the probable errors are large, the difference between them is small, and conversely.
If the psychologists II. and III. were separated by 0.5 and their probable errors were 0.5, as is approximately the case, then the difference between them is so small that there is one chance in four that the position of III. is above the grade of II. If again the psychologists XL. and XLIX. were separated by 6 and their probable errors were 6, as is approximately the case, then there is again one chance in four that the true position of XLIX. is above the grade of XL. The difference between II. and III. is thus about the same as that between XL. and XLIX.
If we take the fifty psychologists in groups of 10, and thus partly eliminate the chance variations, the average probable errors of the five groups are 0.7, 1.8, 4.2, 5.8, 6.2. These probable errors are subject to a correction for the range covered by the grades. Thus the first ten cover a range of about eleven points, and the last ten a range of about six points, and the differences between the psychologists at the top of the list would be nearly twice as great as between those at the bottom of the list if the probable errors were the same. When we take account of both factors, the probable errors in the five groups are 0.6, 1.9, 1.8, 6.4 and 10.7. While the probable errors are determined with a considerable degree of exactness, which is itself measured, the ranges covered by the grades seem to depend on the special conditions in the science; they are not the same in the different sciences, and their validity can not be determined with any exactness. Subject, however, to a considerable probable error, the range of merit covered by the fifty psychologists is inversely as the figures given, and reduced to a scale of 100 would be: 55.6, 17.5, 18.5, 5.2 and 3.2.
Thus we can say that the psychologists at the top of the list are likely to differ from each other about 18 times as much as the psychologists at the bottom of the list. We have no zero point from which we can measure psychological merit. Men who are 6 ft. 2 in. tall are likely to differ from each other
( 703) about ten times as much as men who are about 5 ft. 8 in. tall, though the difference in their height is only as 68:74. Even though we assumed the zero point to be where psychological performance begins or at the survival minimum of human ability, we should only obtain relative differences.
The astronomers and the psychologists have been used as illustrations. The number of students of astronomy and of psychology in the country does not differ greatly, and it is assumed that they represent an equal range of scientific merit. It is possible that it requires more ability to be an astronomer than to be a psychologist, and it is equally possible that, in view of the larger endowments, longer history and more conventional problems, less ability will suffice for the astronomer. The curves of distribution might also vary; for example, it might be relatively easier to be an astronomer of moderate performance, but more difficult to be a great astronomer. There are indications of such differences, but the data at hand do not disclose them with any degree of certainty.
There are 100 geologists and 100 botanists on the list, who are about one fourth of all the geologists and botanists of the country. These are assumed to cover about the same range of scientific merit as the astronomers or the psychologists. The average difference between the geologists would consequently be about half that between the astronomers, and the probable errors of position should theoretically be about twice as large. The anthropologists are the smallest class of scientific men, numbering in all about ninety, of whom 20 are included in the thousand under consideration. They are again assumed to cover a range of performance equal to that of the astronomers or geologists, the average difference between them being two and a half times as great as between the astronomers or five times as great as between the geologists. The chemists are the most numerous class of scientific men, 175 being included in the thousand. There are 150 physicists, 150 zoologists, 80 mathematicians, 60 pathologists, 40 physiologists and 25 anatomists.
In the accompanying table are given the
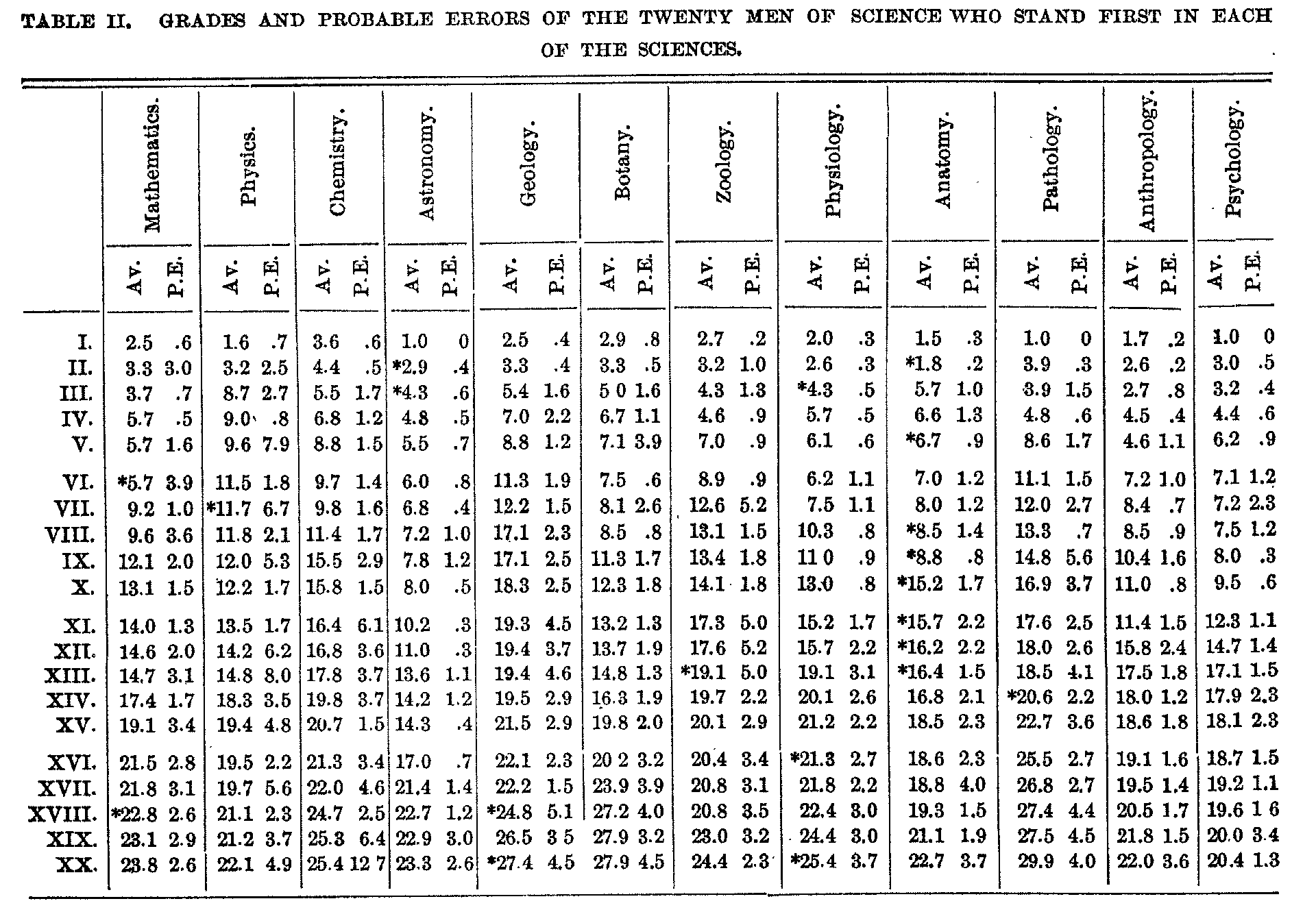
( 704) grades and probable errors of the twenty men of science who were assigned positions at the head of each of the twelve sciences. All the anthropologists are thus included in the table, but only two fifths of the astronomers, one fifth of the geologists, etc. In cases in which an individual stands relatively higher in an-other science a star is attached.
It will be observed that the grades are, as a rule, lower than the positions. As has been stated, the distribution of the judgments or errors in the upper part of the list is `skewed' in a negative direction, so that the average judgment is lower than the median judgment. Further down the list this tendency disappears, and towards the bottom, not given in the table except for the anatomists and anthropologists, the `skew' is in the opposite direction. Chauvenet's criterion has been applied; it causes but an insignificant difference in the order, and for statistical purposes the extra calculations involved were superfluous. As has been explained, however, the incidence of a divergent judgment, which might be due to ignorance or prejudice, might be unjust to an individual. The probable errors have been obtained by taking them directly proportional to the average deviation and assuming that there were always ten judgments. In the comparatively few cases where there were less than ten judgments the probable errors of the average are too small, but the differences are not significant. In the measurement of scientific merit, we are concerned not with the probable error of the average, but with the average probable error, which does not depend on the number of cases. Figures for both might be given, but they are so nearly alike and so lacking in significance that it is not worth while.
As the table shows, there are in astronomy, pathology and psychology men who are placed distinctly at the head. In the other sciences those who stand first have grades varying from 1.6 to 3.6. In most cases the differences in grade are less than the probable errors, or not much larger, and the position is not deter-mined to a single place, though it is deter-mined with a theoretically high degree of validity within a very few places. Various groupings occur, which seem to represent the existing conditions of the sciences. Thus there are breaks of two or more units after chemists 4 and 8; physicist 2; zoologists 4 and 6; geologists 2, 5 and 7; botanist 8; mathematicians 3, 6 and 8; pathologists 1, 4, 5 and 9; psychologist 1; physiologists 7 and 9; anatomists 2 and 9, and anthropologist 5. On the other hand, there are cases in which consecutive numbers are bracketed or practically bracketed. Thus mathematicians 4, 5 and 6 have a grade of 5.7. These various groupings appear to be about what the probable errors would lead us to expect.
The probable errors tend to increase as we go down the lists, but with considerable irregularity. This irregularity is in part due to normal variability where the number of observations is small and the average deviations are relatively large, but the larger departures are usually significant, it being easier to assign a position to some men of science than to others. Thus, for example, it is not easy to compare a man who has made one or two important discoveries with a man who has accomplished a large mass of useful work.
The tendency of the probable errors to in-crease is, however, significant. It is easier to assign the order at the top of the list, and the difficulty increases as we go downward. This subjective fact is measured by the probable errors. It is in part due to less knowledge of those whose work is less important. I know of no way to eliminate this factor or to measure its influence. But the main factor is the real differences between the men, and these are assumed to be inversely as the probable errors and directly as the differences in grade.
In table III. are given all the probable errors averaged in six groups for each of the sciences. In the first and second groups are included one tenth of those in each science, and in the remaining groups one fifth. That is, the probable errors are divided into five equal groups, but the first group is divided into two subgroups, in view of the fact that the probable errors of the first tenth are distinctly smaller than those of the second tenth.
( 705)
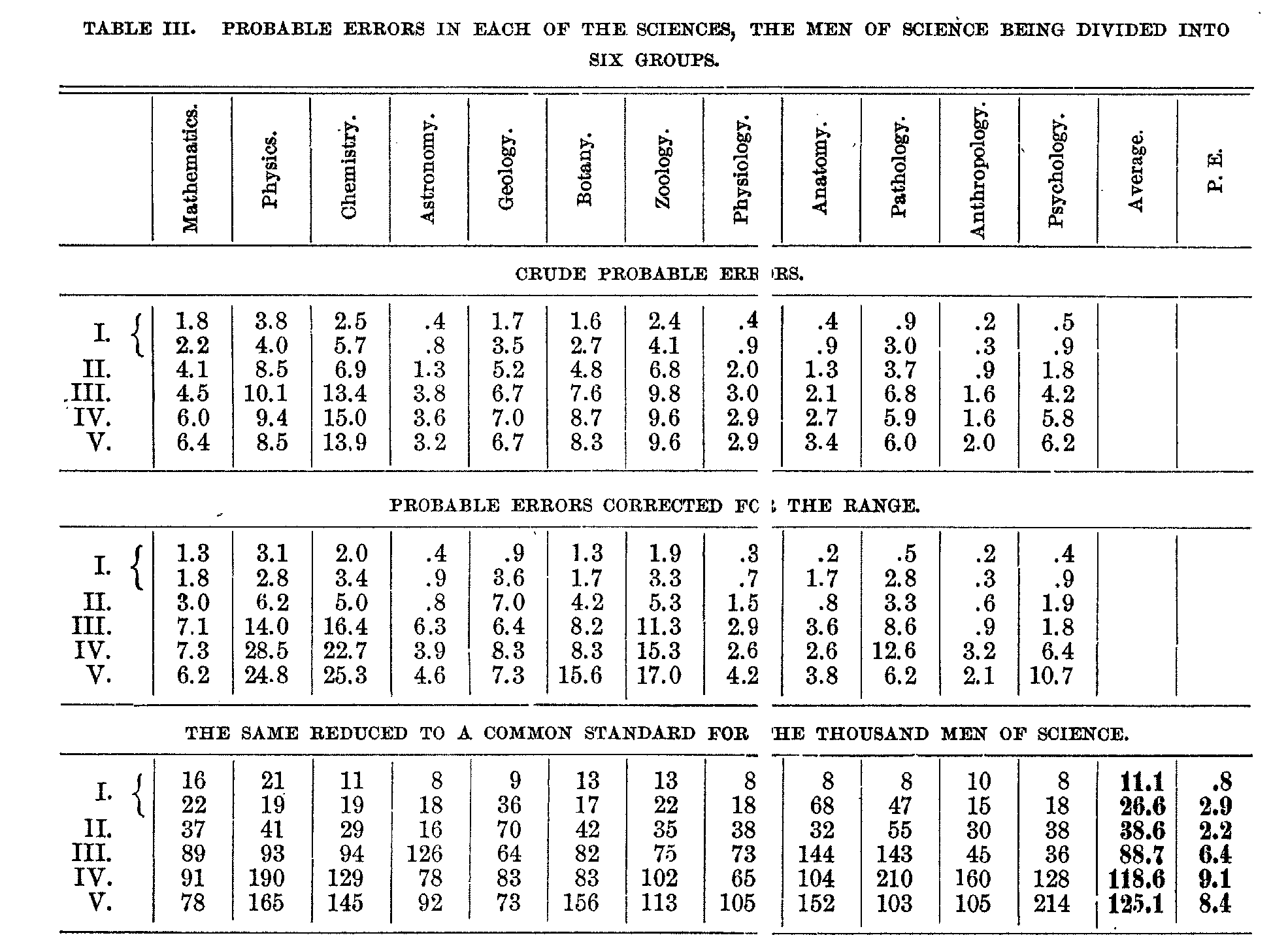
In the middle part of the table the probable errors have been adjusted to the ranges covered by each group, and in the lower part these figures have been reduced to a common standard of a thousand, so that the results for the different sciences may be comparable.
If the range of ability is the same in each science and if the difficulty of assigning the order in each science is the same, then the figures in the lower third of the table should tend to be the same in the different sciences. As the averages include from 2 to 35 cases, they are subject to a probable error which varies considerably. Thus, to take, for ex-ample, an intermediate case-the botanists-the probable errors of the six entries in the upper part of the table are: 0.25, 0.33, 0.18, 0.28, 0.22, 0.25. They thus seem to be determined with considerable validity. When the probable errors are adjusted for the ranges, a considerable ` chance' variation is introduced. If the figures were broken up into groups of different sizes, the results would be different. The figures in the last three groups of each of the sciences seem scarcely to be significant of real differences in the sciences, though they to a certain extent measure the actually existing conditions.
The figures in the table give the validity with which the positions are determined, and at the tame time measure the relative differences 1 between the men in the several groups. Thus the first tenth of the chemists have on the average their positions determined relatively to other chemists with a probable error of two daces and the last fifth with a probable error of 25 places. In relation to the first hundred scientific men, a chemist in this group---has his position determined on the average (apart from the error due to the interpolation) with a probable error of 11 places, whereas in relation to the last 200 scientific men, the place is determined with a probable error of 145 places.
( 706)
The figures also show that the average differences between the chemists who are in the first tenth are about eight times as great as between the chemists towards the middle of the list and about twelve times as great as between the chemists towards the bottom of the list.
As has been stated, there are considerable variations in the figures for the different sciences. In general, however, those in the first hundred differ from each other about ten times as much as those in the last four hundred, among whom there are no constant differences. It is scarcely safe to draw inferences from the variations in the different groups and in the different sciences. If the probable errors in one science were consistently higher than in another, it would mean that in the former science it is more difficult to make the arrangement, which might be due to greater diversity in the work to be compared or to greater similarity in the men. The greater similarity in the men would probably be due to there having been relatively too many men included in that science. But such consistent differences do not appear. Thus the psychologists have the largest probable error in the last group, but the smallest in the third group, and the mathematicians have the second smallest probable error in the last group, 'but the second largest in the first group. In so far as these figures are significant, they might mean that our able psychologists are more able than our able mathematicians, whereas our lesser psychologists are less able than our lesser mathematicians. Itis probably true that our leading psychologists would compare more favorably with those of Germany, France and Great Britain than our leading mathematicians, but inferences as to the variation in the distribution of ability in the different sciences can not be made from the data at hand with any considerable degree of validity. Itwould, however, be of interest to have comparable data for different nations and for different periods.
The workers in the twelve sciences have been combined into one series by interpolation, it being assumed that the range of ability in each science is the same. The probable errors have at the same time been increased to correspond with a thousand cases, as shown in table III. This makes the probable errors relatively correct, but does not allow for the additional chance variations caused by the interpolation. The list is of considerable interest, as it enables us to compare with more or less accuracy men of science working in diverse directions.
The order, grades and probable errors of the fifty who stand first are given to illustrate the method. We can thus say that the work of a certain physicist is equal in value to the work of a certain zoologist, or that a certain
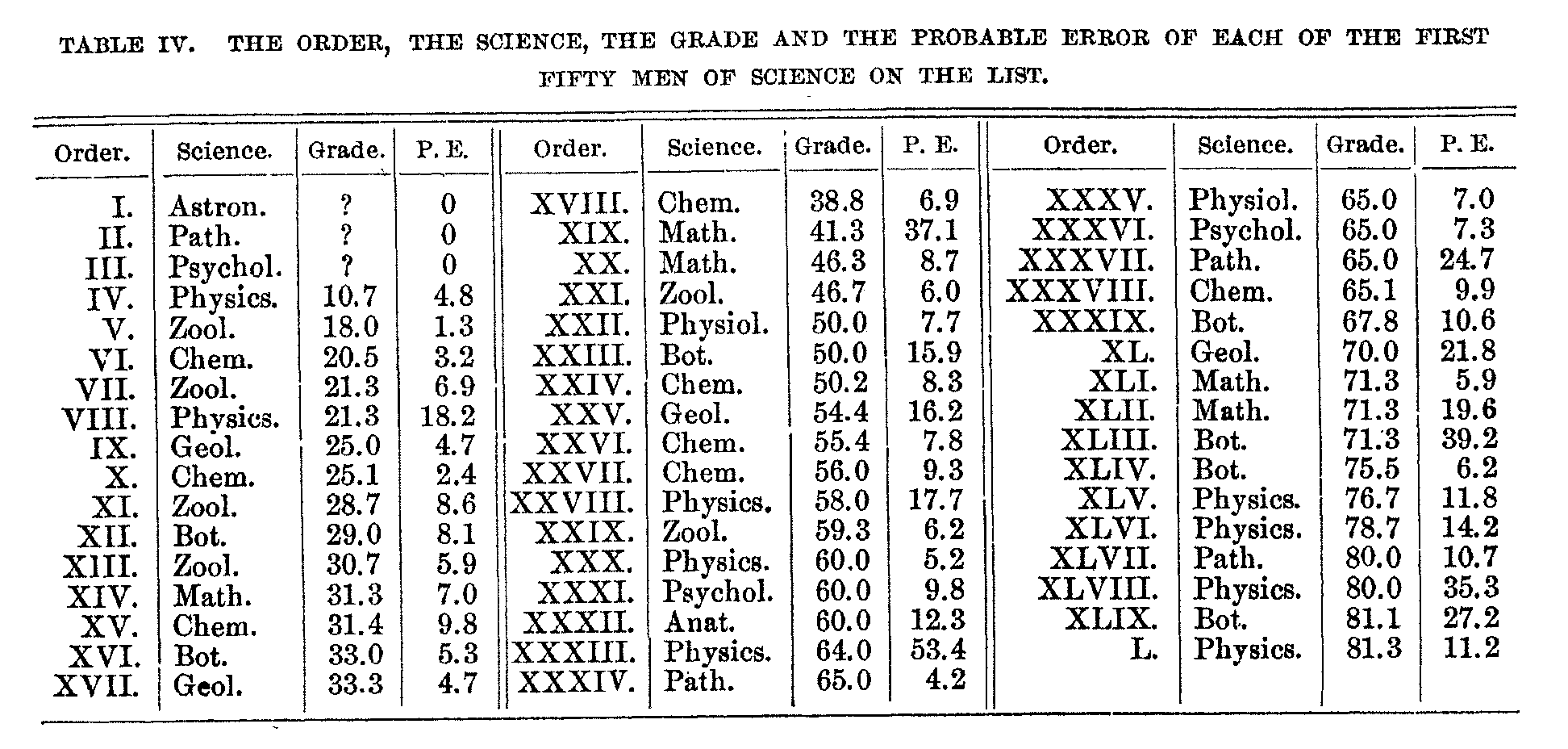
( 706) chemist has one chance in four of being as competent as a certain pathologist, a result that would not be possible by direct comparison. The various factors which limit the exactness of the method should be kept in mind, but we have at least the beginning of a method which with further effort can be made more accurate. Similar methods can be applied to comparing the value of performance in fields even more diverse than the several sciences.
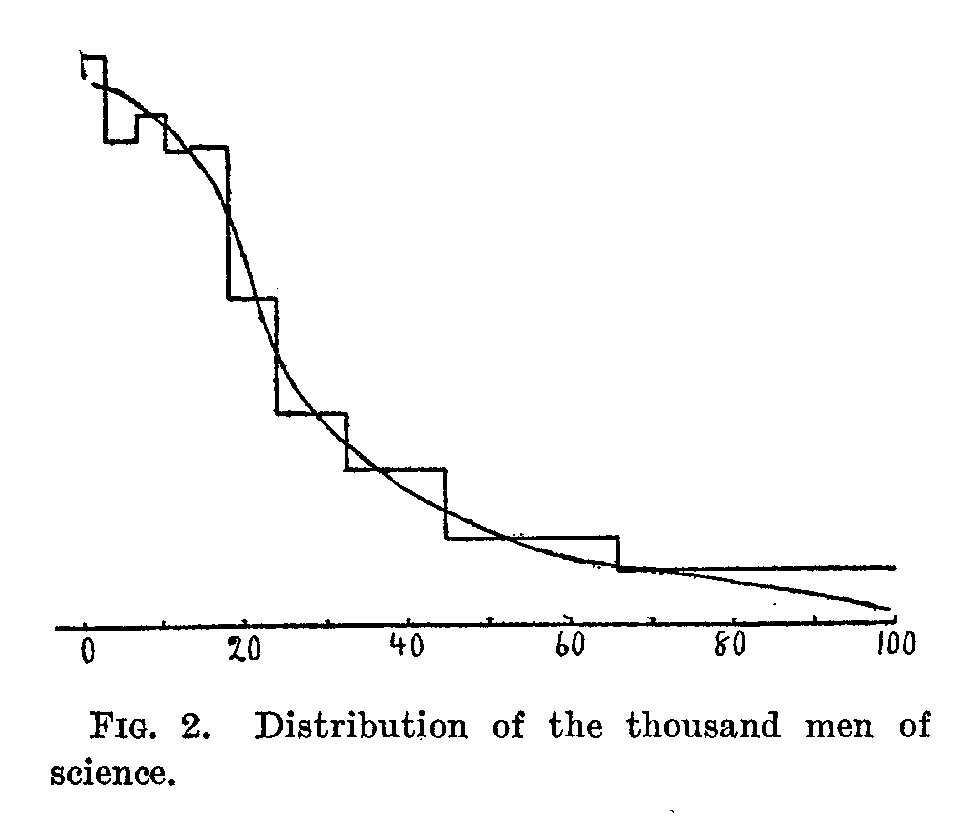
In the accompanying curve-which is based on substantially the same figures as are given in table III., except that a man is given a position only in the science in which he stands the highest-is shown the distribution of the thousand men of science. The 1,000 scientific men are divided into ten groups, the range of eminence or merit covered by each hundred being proportional to the space it occupies on the axis of the abscissas, and the number of each degree of ability being proportional to the ordinates. The range of merit covered by each hundred becomes smaller and there are more of each degree of merit as we pass from the first to the second hundred and so on for the first five hundred, after which the differences become very small. The first hundred men of science cover a range of merit about equal to that of the second and third hundreds together, and this again is very nearly equal to the range covered by the remaining seven hundred. The average differences between the men in the first hundred are about twice as great as between the men in the second and third hundreds, and about seven times as great as between the men in the remaining groups. Or the differences among the first hundred are almost exactly ten times as great as among the last five hundred, who differ but little among themselves. It would be desirable to compare this distribution with that of the normal probability integral and with the salaries paid to scientific men, but the data are not as yet at hand.
J. MCKEEN CATTELL.
COLUMBIA UNIVERSITY.