Solutions to :

Seismic Waves

Back to Earthquake Math Trail Home
Richter Scale

See the site map
Casualties
Tsunamis
Quake-Proofing
Earthquake Preparation
Earthquake Insurance

Seismic Waves (to top menu)

1) d=vt
t = 600km / 6km/s
t= 100 sec( it takes 100 sec for the P wave to reach Vancouver)

d= vt
t= 600km/4km/s
t= 150 sec ( it takes 150 sec for S wave to reach Vancouver)

Therefore the P wave reaches Vancouver 50 sec faster than S wave.
2) With an increase in distance, the range of P and S wave increases over time.
3) Closest: Vernon(44 sec), Nelson(56 sec), Cranbrook (70 sec)
4) 390 km for an SP interval of 40 sec
5) slope: rise/run
(61sec - 35sec ) / (600km- 340km)
slope: 1/10
6) You would need a minimum of two circles because the tangent of two circles will represent an epicenter.
7) Looking at the map with the three circles, any point lying on the green circle is a potential epicentre.
8) The three circles should intersect near Port Alberni.

(x-4.5)2 + (y+4.5)2 = 46.93 ( Cranbook )
(x-1.85)2 + (y+3.23)2 = 18.49 (Vernon)
(x-3.02)2 + (y+4.08)2 = 29.16 (Nelson)

Sample of work:
1 unit on the grid is roughly equivalent to 100Km.
The radius of the circle is derived from using the Sp standard graph.  For example the seismogram of Cranbrook indicates that the epicentre is about 685Km away. This is equivalent to 6.85units. The squared of 6.85= 46.93.

The orgin of each city is derived by estimating with a ruler the x and y coordinates.
C
H
A
L
L
E
N
G
E
a) Bella Coola is 558km away from Victoria. Using the SP standard graph, this corresponds to an S-P interval of 58 sec.
b) Kelowna is 378 km away from Victoria. This corresponds to an S-P interval of 39 sec.
c) Vancouver is 98 km away from Victoria. This corresponds to an S-P interval of 10 sec.

 

Richter Scale (to top menu)

1) 100 times (10 X 10).
2) 1000 times (10 X 10 X 10).
3) 5.01 times.
4) 6.31 X 105 times.
5) 1.12 X 1013 kWh.
6) 3.16 X 1013 kWh.
7) 3.61 X 1013 years.

Casualties (to top menu)

1) Mean = 16140, Median = 4000, Mode = 4000.
2) Maximum = 8.2, Mean = 7.35.
3) In general, the greater the magnitude of the earthquake, the larger the number of casualties.
4) Answers may vary. Plot may appear highly exponential (beginning low and increasing quickly).
5) Answers will vary greatly depending on accuracy of the scatter plot, and function used for approximation.

Tsunamis (to top menu)

1) Plugging 4500 m into the wave-speed equation, the answer is equal to:
c = sqrt (9.8 x 4500) = 210 m/s
Converting this into km/h: 210 m/s x (1 km/1000 m) x (3600 s/h) = 756 km/h
2)

d
(m)

c
(m/s)

c
(m/s)
1000 99 356
5029 222 800
6000 242 873

Quake-Proofing (to top menu)

1)

Assuming we install one beam in each rectangle, on the sides of the building, we will need 12 beams in total: 6 longer beams and 6 shorter beams.

The length of a beam may be found by using the Pythagorean Triangle property: a2 + b2 = c2

Therefore, the length of a longer beam is equal to: sqrt(152 + 102) = sqrt(325) = 18.03 m

Likewise, the length of a shorter beam is equal to: sqrt(102 + 102) = sqrt(200) = 14.14 m

The total beam length is equal to : (6 x 18.03) + (6 x 14.14) = 193.03 m

The cost, therefore, is equal to: $1000/m x 193.03 m = $193,030
2)

Half of the total beam length from the previous is equal to: 193.03/2 = 96.52 m

The cost, therefore, is equal to: $1900/m x 96.52 m = $183,378

The amount of money saved is equal to: $193,030 - 183,378 = $9,652
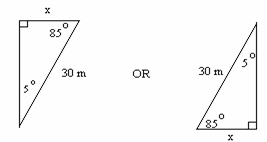
3) Draw a simple triangle relating the initial and final positions of the person.

The horizontal distance, x, may be calculated as:
x = 30 sin(5o) or x = 30 cos(85o) = 2.61 m

4) Assuming the Transamerica building swayed approximately 1ft from side to side, it is safe to say that a horizontal displacement of 2.61 m is greater than 1 ft. The answer, therefore, is YES.

Earthquake Preparation (to top menu)

1) (72 hours)(60min/hour)(60min/sec) = 259200 seconds.
2) (4mL)/(4500mL) = .08889%.
3) d = 4.9 t2 => 3m = 4.9 t2 => t = .7824s.
v = 9.8t => v = 9.8(.7824s) => 7.6681m/s.

Earthquake Insurance (to top menu)

1)
a) 0.9($35,000) = $31,500.
b) 0.1($35,000) = $3,500.
2)
a) $334 US dollars => $334(1.41) = $470.94.
b)

(258-220)/(120,000-100,000) = .0019

(220-193)/(100,000-80,000) = .00135

The slope of the two secant lines are unequal, therefore the relationship is not linear.
c) 3
d) Individual graphs may vary. It is neither uniformly increasing or decreasing.

Back to Earthquake Math Trail Home