A Technique For Determining the Optimum Rating Scale of Opinion Measures
H. Earl Pemberton
Fellow in Sociology, University of
Southern California
H. EARL PEMBERTON
THE OBJECT of this study was to determine the optimum rating scale for a measure of group opinion. The opinion test for which a scale was desired is a series of twenty statements of possible legislative policy, for example: "The United States should adopt a general two per cent sales tax "A legal dismissal wage in industry is desirable in the United States." A rating scale was to be used by which those taking the test were to indicate the degree of their favorableness or opposition to the proposal. To clarify the problem we present a sample scale:
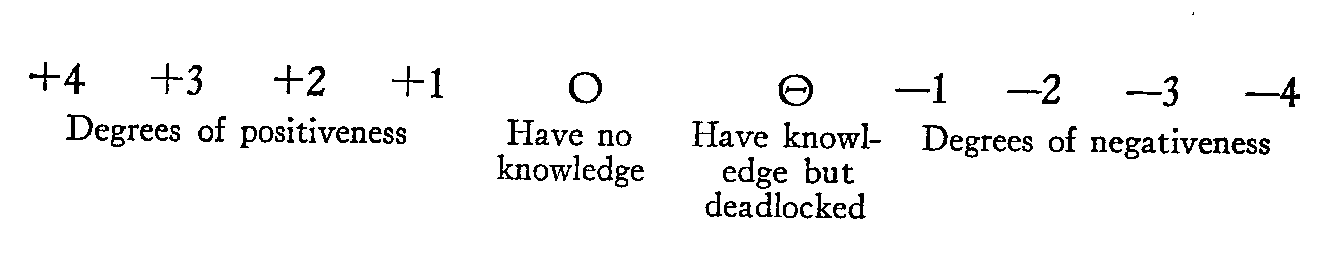
Our problem was to determine how coarse or how fine a scale would give the highest reliability to the measure; that is, should the scale range from +4 to -4 as does the sample above, or should it be finer, ranging from +5 to -5, or coarser, ranging from +3 to -3, or from +2 to -2.
Previous studies in the measurement of opinion by the use of a scale have used scales ranging from two points as
( 471) high as five points each side of a neutral position.[1] No one of these studies appears to consider the relative desirability of different size scales.
A coarse scale is generally more readily used than a fine scale. Hence, the coarse scale was regarded as more desirable if its use did not result in too great a loss of re-liability. Our problem was then to determine how coarse a scale we could use without lowering reliability beyond an arbitrary limit. This limit which we adopted was as follows : Loss in reliability permitted in order to make rating easier is the loss equivalent to a drop from .91 to .90.[2]
Our next problem was to devise a means for determining the reliability of the test. Four sets of the test of twentyitems were made, each with a different scale. The scales were from +2 to -2, +3 to -3, +4 to -4, and +5 to -5. These tests were given to 450 students in classes at the University of Southern California. Each class was divided into four equal parts and each fourth given one of the scales. Two days after he had first taken the test, each
( 472) student was given the same scale which he had taken previously. When the tests were given for the second time, the purpose of the experiment was explained to the students. Instructions were given that these second tests were not to be answered by attempted recall of what was answered the previous time. While there was, no doubt, considerable retention of what had been answered the first time, this factor was regarded as constant for each of the four scales.
We then correlated the first answers of each student to items 1, 5, 10, 15, and 20 with that student's answers the second time he took the test. All answers on the same scale were used in one correlation. Four correlations for reliability were thus obtained. The results were as follows :
Scale 2 to -2: .75 +.01
3 to -3 : .82 +.01
4 to -4 : .791+.01
5 to -5 : .796+.01
According to the criteria adopted above, the scale from 3 to -3 is most desirable for this test. This scale has a higher reliability than either of the finer scales. Since coarseness is more desirable than fineness these finer scales are discarded. The scale from +2 to -2 has a reliability of .75-.01. This falls .07 below the reliability of the +3 scale. This drop is beyond the limit decided as permissable for the mere purpose of making the rating easier by making the scale coarser. This limit for a test with a reliability of .82 is about .805.
While a scale from 3 to -3 is most desirable for this particular measure of
opinion there is no assurance that it would- be so for other tests. It appears
probable that tests using such a scale plan should each be tested by some such
method as the above to determine the most desirable scale.