A Law of Comparative Judgment
Louis L. Thurstone
University of Chicago
The object of this paper is to describe a new psycho-physical law which may be called the law of comparative judgment and to show some of its special applications in the ,measurement of psychological values. The law of comparative judgment is implied in Weber's law and in Fechner's law. The law of comparative judgment is applicable not only to the comparison of physical stimulus intensities but also to qualitative comparative judgments such as those of excellence of specimens in an educational scale and it has been applied in the measurement of such psychological values as a series of opinions on disputed public issues. The latter application of the law will be illustrated in a forthcoming study. It should be possible also to verify it on comparative judgments which involve simultaneous and successive contrast.
The law has been derived in a previous article and the present study is mainly a description of some of its applications. Since several new concepts are involved in the formulation of the law it has been necessary to invent several terms to describe them, and these will be repeated here.
Let us suppose that we are confronted with a series of stimuli or specimens such as a series of gray values, cylindrical weights, handwriting specimens, children's drawings, or any other series of stimuli that are subject to comparison. The first requirement is of course a specification as to what it is, that we are to judge or compare. It may be gray values, or weights, or excellence, or any other quantitative or qualitative attribute about which we can think `more' or `less' for each specimen. This attribute which may be assigned, as it were, in differing amounts to each specimen defines what we shall call the psychological continuum for that particular project in measurement.
( 274)
As we inspect two or more specimens for the task of comparison there must be some kind of process in us by which we react differently to the several specimens, by which we identify the several degrees of excellence or weight or gray value in the specimens. You may suit your own predilections in calling this process psychical, neural, chemical, or electrical but it will be called here in a non-committal way the discriminal process because its ultimate nature does not concern the formulation of the law of comparative judgment. If then, one handwriting specimen seems to be more excellent than a second specimen, then the two discriminal processes of the observer are different, at least on this occasion.
The so-called `just noticeable difference' is contingent on the fact that an observer is not consistent in his comparative judgments from one occasion to the next. He gives different comparative judgments on successive occasions about the same pair of stimuli. Hence we conclude that the discriminal process corresponding to a given stimulus is not fixed. It fluctuates. For any handwriting specimen, for example, there is one discriminal process that is experienced more often with that specimen than other processes which correspond to higher or lower degrees of excellence. This most common process is called here the modal discriminal process for the given stimulus.
The psychological continuum or scale is so constructed or defined that the frequencies of the respective discriminal processes for any given stimulus form a normal distribution on the psychological scale. This involves no assumption of a normal distribution or of anything else. The psychological scale is at best an artificial construct. If it has any physical reality we certainly have not the remotest idea what it may be like. We do not assume, therefore, that the distribution of discriminal processes is normal on the scale because that would imply that the scale is there already. We define the scale in terms of the frequencies of the discriminal processes for any stimulus. This artificial construct, the psychological scale, is so spaced off that the frequencies of the discriminal processes for any given stimulus form a normal distribution
( 275) on the scale. The separation on the scale between the discriminal process for a given stimulus on any particular occasion and the modal discriminal process for that stimulus we shall call the discriminal deviation on that occasion. If on a particular occasion, the observer perceives more than the usual degree of excellence or weight in the specimen in question, the discriminal deviation is at that instant positive. In a similar manner the discriminal deviation at another moment will be negative.
The standard deviation of the distribution of discriminal processes on the scale for a particular specimen will be called its discriminal dispersion.
This is the central concept in the present analysis. An ambiguous stimulus which is observed at widely different degrees of excellence or weight or gray value on different occasions will have of course a large discriminal dispersion. Some other stimulus or specimen which is provocative of relatively slight fluctuations in discriminal processes will have, r similarly, a small discriminal dispersion.
The scale difference between the discriminal processes of two specimens which are involved in the same judgment will be called the discriminal difference on that occasion. If the two stimuli be denoted A and B and if the discriminal processes corresponding to them be denoted a and b on any one occasion, then the discriminal difference will be the scale distance (a — b) which varies of course on different occasions. If, in one of the comparative judgments, A seems to be better than B, then, on that occasion, the discriminal difference (a — b) is positive. If, on another occasion, the stimulus B seems to be the better, then on that occasion the discriminal difference (a — b) is negative.
Finally, the scale distance between the modal discriminal processes for any two specimens is the separation which is assigned to the two specimens on the psychological scale. The two specimens are so allocated on the scale that their separation is equal to the separation between their respective modal discriminal processes.
We can now state the law of comparative judgment as follows:
( 176)
![]()
in which
Si and S2 are the psychological scale values of the two compared stimuli.
x12 = the sigma value corresponding to the proportion of judgments p1>2. When p1>2 is greater than .50 the numerical value of x12 is positive. When p1>2 is less than .50 the numerical value of x12 is negative.
σ1 = discriminal dispersion of stimulus Rl.
σ2 = discriminal dispersion of stimulus R2
r = correlation between the discriminal deviations of R1 and R2 in the same judgment.
This law of comparative judgment is basic for all experimental work on Weber's law, Fechner's law, and for all educational and psychological scales in which comparative judgments are involved. Its derivation will not be repeated here because it has been described in a previous article.[2] It applies fundamentally to the judgments of a single observer who compares a series of stimuli by the method of paired comparison when no `equal' judgments are allowed. It is a rational equation for the method of constant stimuli. It is assumed that the single observer compares each pair of stimuli a sufficient number of times so that a proportion, pa>a, may be determined for each pair of stimuli.
For the practical application of the law of comparative judgment we shall consider five cases which differ, in assumptions, approximations, and degree of simplification. The more assumptions we care to make, the simpler will be the observation equations. These five cases are as follows:
Case I.—The equation can be used in its complete form for paired comparison data obtained from a single subject when only two judgments are allowed for each observation such as `heavier' or `lighter,' `better' or `worse,' etc. There will be one observation equation for every observed proportion of judgments. It would be written, in its complete form, thus:
< insert formula 1 >
( 177)
According to this equation every pair of stimuli presents the possibility of a different correlation between the discriminal deviations. If this degree of freedom is allowed, the problem of psychological scaling would be insoluble because every observation equation would introduce a new unknown and the number of unknowns would then always be greater than the number of observation equations. In order to make the problem soluble, it is necessary to make at least one assumption, namely that the correlation between discriminal deviations is practically constant throughout the stimulus series and for the single observer. Then, if we have n stimuli or specimens in the scale, we shall have 2 n(n — I) observation equations when each specimen is compared with every other specimen. Each specimen has a scale value, S,, and a discriminal dispersion, al, to be determined. There are therefore 2n unknowns. The scale value of one of the specimens is chosen as an origin and its discriminal dispersion as a unit of measurement, while r is an unknown which is assumed to be constant for the whole series. Hence, for a scale of n specimens there will be (2n — i) unknowns. The smallest number of specimens for which the problem is soluble is five. For such a scale there will be nine unknowns, four scale values, four discriminal dispersions, and r. For a scale of five specimens there will be ten observation equations.
The statement of the law of comparative judgment in the form of equation I involves one theoretical assumption which is probably of minor importance. It assumes that all positive discriminal differences (a — b) are judged A > B, and that all negative discriminal differences (a — b) are judged A < B. This is probably not absolutely correct when the discriminal differences of either sign are very small. The assumption would not affect the experimentally observed proportion p A> a if the small positive discriminal differences occurred as often as the small negative ones. As a matter of fact, when p A> a is greater than .50 the small positive discriminal differences (a — b) are slightly more frequent than the negative perceived differences (a — b). It is probable that rather refined experimental procedures are necessary to
( 178) isolate this effect: The effect is ignored in our present analysis.
Case II.—The law of comparative judgment as described under Case I refers fundamentally to a series of judgments of a single observer. It does not constitute an assumption to say that the discriminal processes for a single observer give a normal frequency distribution on the psychological continuum. That is a part of the definition of the psychological scale. But it does constitute an assumption to take for granted that the various degrees of an attribute of a specimen perceived in it by a group of subjects is a normal distribution. For example, if a weight-cylinder is lifted by an observer several hundred times in comparison with other cylinders, it is possible to define or construct the psychological scale so that the distribution of the apparent weights of the cylinder for the single observer is normal. It is probably safe to assume that the distribution of apparent weights for a group of subjects, each subject perceiving the weight only once, is also normal on the same scale. To transfer the reasoning in the same way from a single observer to a group of observers for specimens such as handwriting or English Composition is not so certain. For practical purposes it may be assumed. that when a group of observers perceives a specimen of hand-writing, the distribution of excellence that they read into the specimen is normal on the psychological continuum of perceived excellence. At least this is a safe assumption if the group is not split in some curious way with prejudices for or against particular elements of the specimen.
With the assumption just described, the law of comparative judgment, derived. for the method of constant stimuli. with two responses, can be extended to data collected from a group of judges in which each judge compares, each stimulus with every other stimulus only once. The other assumptions of Case I apply also to Case II.
Case III.—Equation 1 is awkward to handle as an observation equation for a scale. with a large number of specimens. In fact the, arithmetical labor of constructing an educational or psychological scale with it is almost prohibitive. The
( 179) equation can be simplified if the correlation r can be assumed to be either zero or unity. It is a safe assumption that when the stimulus series is very homogeneous with no distracting attributes, the correlation between discriminal deviations is low and possibly even zero unless we encounter the effect of simultaneous or successive contrast. If we accept the correlation as zero, we are really assuming that the degree of excellence which an observer perceives in one of the specimens has no influence on the degree of excellence that he perceives in the comparison specimen. There are two effects that may be operative here and which are antagonistic to each other.
(1) If you look at two handwriting specimens in a mood slightly more generous and tolerant than ordinarily, you may perceive- a degree of excellence in specimen A a little higher than its mean excellence. But at the same moment specimen B is also judged a little higher than its average or mean excellence for the same reason. To the extent that such a factor is at work the discriminal deviations will tend to vary together and the correlation r will be high and positive.
(2) The opposite effect is seen in simultaneous contrast. When the correlation between the discriminal deviations is negative the law of comparative judgment gives an exaggerated psychological difference (Sl— S2) which we know as simultaneous or successive contrast. In this type of comparative judgment the discriminal deviations are negatively associated. It is probable that this effect: tends to be a minimum when the specimens have other perceivable attributes, and that it is a maximum when other distracting stimulus differences are removed. If this statement should be experimentally verified, it would constitute an interesting generalization in perception.
If our last generalization is correct, it should be a safe assumption to write r = 0 for those scales in which the specimens are rather complex such as handwriting specimens and childrens’ drawings. If we look at two handwriting specimens and perceive one of them as unusually fine, it probably tends to depress somewhat the degree of excellence
( 180) we would ordinarily perceive in the comparison specimen, but this effect is slight compared with the simultaneous contrast perceived in lifted weights and in gray values. Furthermore, the simultaneous contrast is slight with small stimulus differences and it must be recalled that psycho-logical scales are based on comparisons in the subliminal or barely supraliminal range.
The correlation between discriminal deviations is probably high when the two
stimuli give simultaneous contrast and are quite far apart on the scale. When
the range for the correlation is reduced to a scale distance comparable with the
difference limen, the correlation probably is reduced nearly to zero. At any
rate, in order to simplify equation i we shall assume that it is zero. This
represents the comparative judgment in which the evaluation of one of the
specimens has no influence on the evaluation of the other specimen in the paired
judgment. The law then takes the following form.
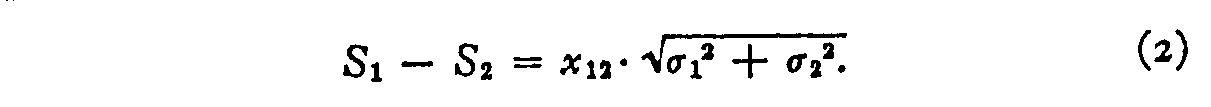
Case IV.—If we can make the additional assumption that the discriminal dispersions are not subject to gross variation, we can considerably simplify the equation so that it becomes linear and therefore much easier to handle. In equation (2) we let
σ2 = σ1+d,
in which d is assumed to be at least smaller than al and preferably a fraction of σ1 such as .1 to .5. Then equation (2) becomes
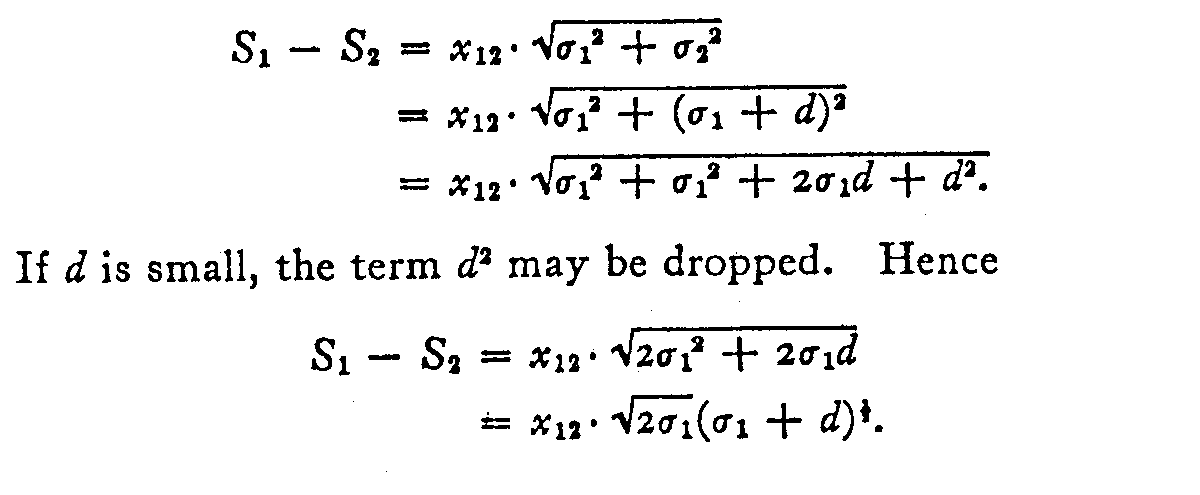
(181)
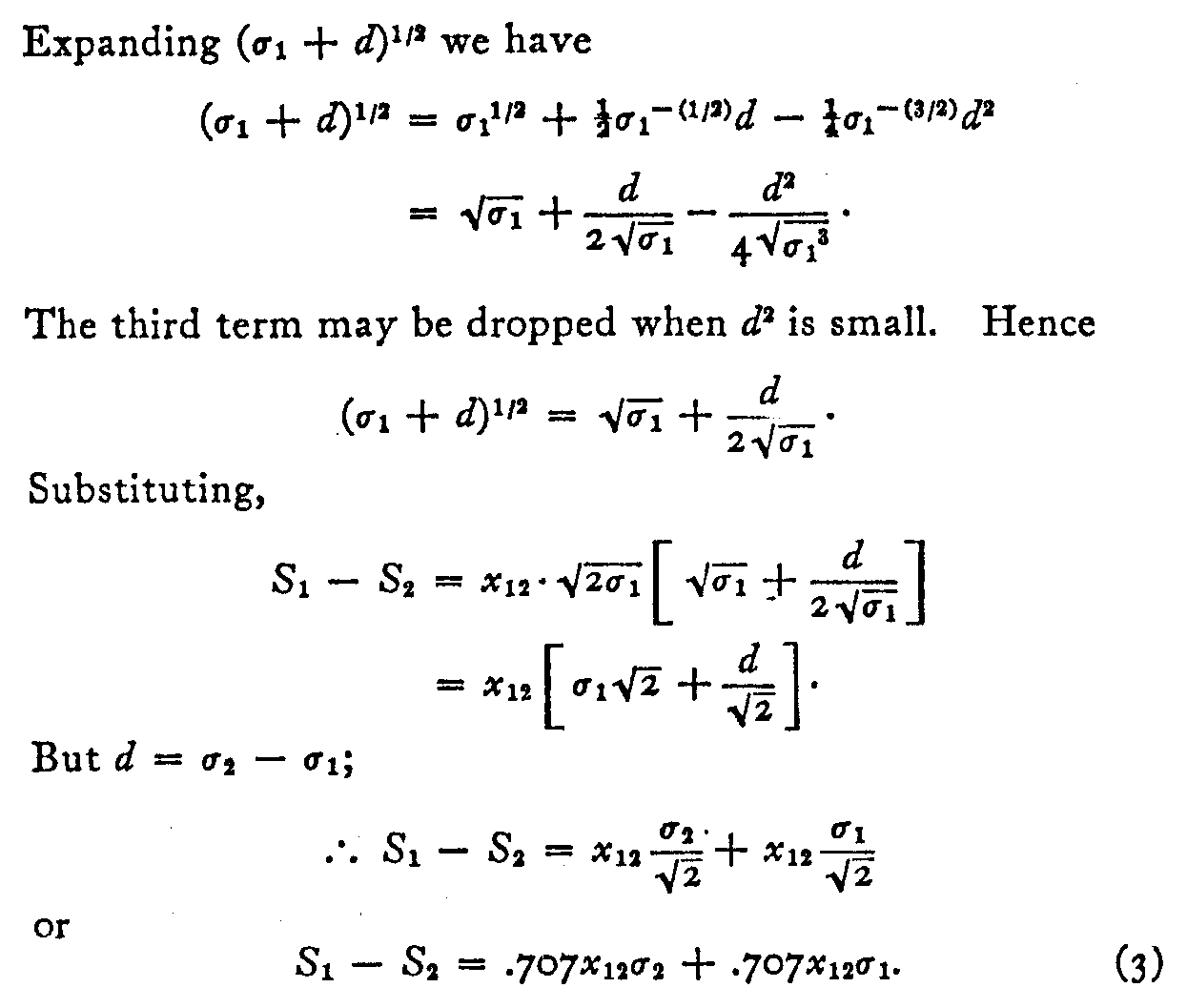
Equation (3) is linear and very easily handled. If σ2 – σ1 is small compared with σ1, equation (3) gives a close approximation to the true values of S and σ for each specimen.
If there are n stimuli in the scale there will be (2n – 2) unknowns, namely a scale value S and a discriminal dispersion σ for each specimen. The scale value for one of the specimens may be chosen as the origin or zero since the origin of the psychological scale is arbitrary. The discriminal dispersion of the same specimen may be chosen as a unit of measurement for the scale. With n specimens in the series there will be ˝ n(n – 1) observation equations. The minimum number of specimens for which the scaling problem can be solved is then four, at which number we have six observation equations and six unknowns.
Case V.—The simplest case involves the assumption that all the discriminal dispersions are equal. This may be legitimate for rough measurement such as Thorndike's hand-
( 282) -writing scale or the Hillegas scale of English Composition. Equation (2) then becomes
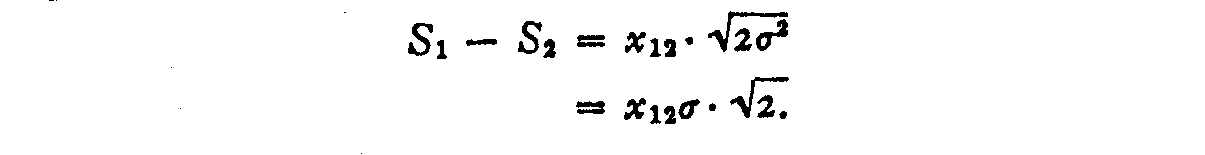
But since the assumed constant discriminal dispersion is the unit of
measurement we have
S1– S2 = 1.4142x12.(4)
This is a simple observation equation which may be used for rather coarse scaling. It measures the scale distance between two specimens as directly proportional to the sigma value of the observed proportion of judgments pl>2. This is the equation that is basic for Thorndike's procedure in scaling handwriting and children's drawings although he has not shown the theory underlying his scaling procedure. His unit of measurement was the standard deviation of the discriminal differences which is .707σ when the discriminal dispersions are constant. In future scaling problems equation (3) will probably be found to be the most useful.WEIGHTING THE OBSERVATION EQUATIONS
The observation equations obtained under any of the five cases are not of the same reliability and hence they should not all be equally weighted. Two observed proportions of judgments such as pl>2 = .99 and pl>3 = .55 are not equally reliable. The proportion of judgments pl>2 is one of the observations that determine the scale separation between Sl and S2. It measures the scale distance (S1— S2) in terms of the standard deviation, σ1–2, of the distribution of discriminal differences for the two stimuli RI and R2. This distribution is necessarily normal by the definition of the psychological scale.
The standard error of a proportion of a normal frequency distribution is
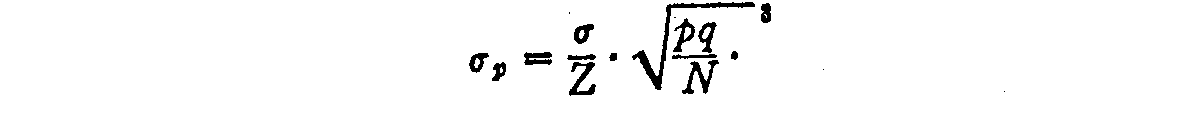
(283) in which a is the standard deviation of the distribution, Z is the ordinate corresponding to p, and q = 1–p while N is the number of cases on which the proportion is ascertained. The term a in the present case is the standard deviation al—2 of the distribution of discriminal differences. Hence the standard error of p1>2 is
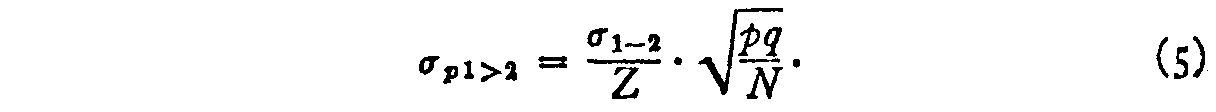
But since, by equation (2)
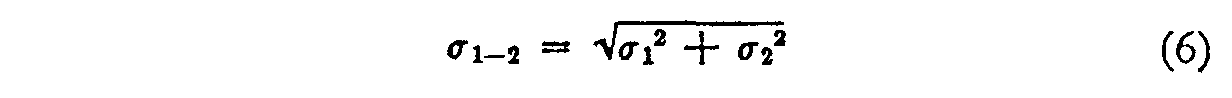
and since this may be written approximately, by equation (3), as
σ1–2
= .707(σ1 + σ2) (7)
we have
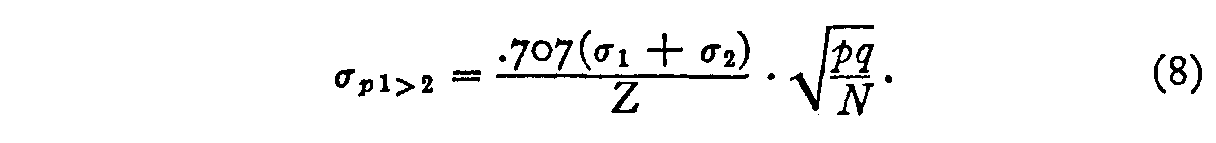
The weight, wl–2, that should be assigned to observation equation (2) is the reciprocal of the square of its standard error. Hence
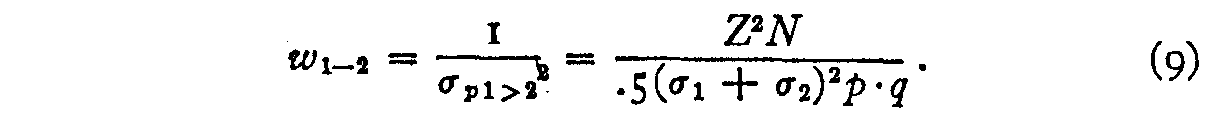
It will not repay the trouble to attempt to carry the factor (σl + σ2)2 in the formula because this factor contains two of the unknowns, and because it destroys the linearity of the observation equation (3), while the only advantage gained would be a refinement in the weighting of the observation equations. Since only the weighting is here at stake, it may be approximated by eliminating this factor. The factor .5 is a constant. It has no effect, and the weighting then becomes
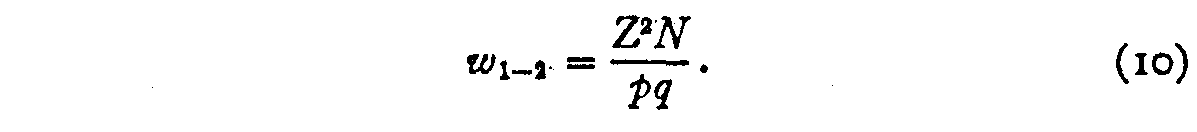
By arranging the experiments in such a way that all the observed proportions are based on the same number of judgments the factor N becomes a constant and therefore has
(
284) no effect on the weighting. Hence
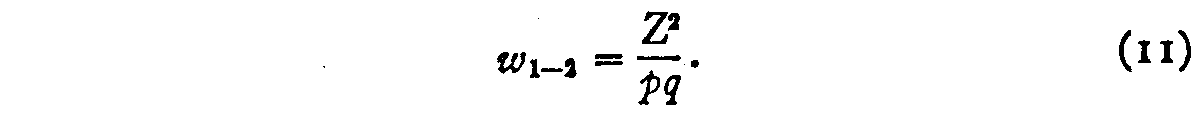
This weighting factor is entirely determined by the proportion, p1>2 of
judgments ` I is better than 2' and it can therefore be readily ascertained by
the Kelley-Wood tables. The weighted form of observation equation (3) therefore
becomes
wS1 – wS2 – .707wx12σ2 – .707wx12σ1 = o.(12)
This equation is linear and can therefore be easily handled. The coefficient .707wx12 is entirely determined by the observed value of p for each equation and therefore a facilitating table can be prepared to reduce the labor of setting up the normal equations. The same weighting would be used for any of the observation equations in the five cases since the weight is solely a function of p when a factor is ignored for the weighting formula.SUMMARY
A law of comparative judgment has been formulated which is expressed in its complete form as equation (I). This law defines the psychological scale or continuum. It allocates the compared stimuli on the continuum. It expresses the experimentally observed proportion, p1>2 of judgments ‘I is stronger (better, lighter, more excellent) than 2 ' as a function of the scale values of the stimuli, their respective discriminal dispersions, and the correlation between the paired discriminal deviations.
The formulation of the law of comparative judgment involves the use of a new psychophysical concept, namely, the discriminal dispersion. Closely related to this concept are those of the discriminal process, the modal discriminal process, the discriminal deviation, the discriminal difference. All of these psychophysical concepts concern the ambiguity or qualitative variation with which one stimulus is perceived by the same observer on different occasions.
The psychological scale has been defined as the particular linear spacing of the confused stimuli which yields a normal
( 285) distribution of the discriminal processes for any one of the stimuli. The validity of this definition of the psychological continuum can be experimentally and objectively tested. If the stimuli are so spaced out on the scale that the distribution of discriminal processes for one of the stimuli is normal, then these scale allocations should remain the same when they are defined by the distribution of discriminal processes of any other stimulus within the confusing range. It is physically impossible for this condition to obtain for several psychological scales defined by different types of distribution of the discriminal processes. Consistency can be found only for one form of distribution of discriminal processes as a basis for defining the scale. If, for example, the scale is defined on the basis of a rectangular distribution of the discriminal processes, it is easily shown by experimental data that there will be gross discrepancies between experimental and theoretical proportions, p1>2. The residuals should be investigated to ascertain whether they are a minimum when the normal or Gaussian distribution of discriminal processes is used as a basis for defining the psychological scale. Tri-angular and other forms of distribution might be tried. Such an experimental demonstration would constitute perhaps the most fundamental discovery that has been made in the field of psychological measurement. Lacking such proof and since the Gaussian distribution of discriminal processes yields scale values that agree very closely with the experimental data, I have defined the psychological continuum that is 1-implied in Weber's Law, in Fechner's Law, and in educational quality scales as that particular linear spacing of the stimuli which gives a Gaussian distribution of discriminal processes.
The law of comparative judgment has been considered in this paper under five cases which involve different assumptions and degrees of simplification for practical use. These may be summarized as follows.
Case I.—The law is stated in complete form by equation (I). It is a rational equation for the method of paired comparison. It is applicable to all problems involving the method of constant stimuli for the measurement of both
( 286) quantitative and qualitative stimulus differences. It concerns the repeated judgments of a single observer.
Case II.—The same equation (1) is here used for a group of observers, each observer making only one judgment for each pair of stimuli, or one serial ranking of all the stimuli. It assumes that the distribution of the perceived relative values of each stimulus is normal for the group of observers.
Case III.—The assumptions of Cases I. and II. are involved here also and in addition it is assumed that the correlation between the discriminal deviations of the same judgment are uncorrelated. This leads to the simpler form of the law in equation (2).
Case IV.—Besides the preceding assumptions the still simpler form of the law in equation (3) assumes that the discriminal deviations are not grossly different so that in general one may write
σ2 — σl < σl
and that preferably
σ2 — σl=d
in which d is a small fraction of σl.
Case V.—This is the simplest formulation of the law and it involves, in addition to previous assumptions, the assumption that all the discriminal dispersions are equal. This assumption should not be made without experimental test. Case V. is identical with Thorndike's method of constructing quality scales for handwriting and for children's drawings. His unit of measurement is the standard deviation of the distribution of discriminal differences when the discriminal dispersions are assumed to be equal.
Since the standard error of the observed proportion of judgments, p1>2,
is not uniform, it is advisable to weight each of the observation equations by a
factor shown in equation (II) which is applicable to the observation equations
in any of the five cases considered. Its application to equation (3) leads to
the weighted observation equation (12).