Handwriting
The Measurement of the Quality of Handwriting
Edward L. Thorndike
Previous
Section 2. The Construction of a Scale for Quality of Handwritings of Children in Grades 5 to 8
If one selects from children's written work from samples ranging from the best to the worst handwriting found in grades 5 to 8 and tries to rank these 1000 samples in order of merit for handwriting, one finds that he cannot make 1000 such ranks. Some of the handwritings will be indistinguishable in " goodness " or "quality" or "merit." Nor can one make 100 such ranks. Nor can one make 40. One can make about 20, but if he so ranks the samples a number of times he gets substantially the same average result as he gets when he ranks them a number of times in 10 or 11 groups. To get an individual's judgment of the relative merits of the 1000 samples it is sufficient to have him rank them in 10 or 11 groups three or four times. If he grades in 10 groups and tries to make the differences in " goodness" or "quality" or "merit" all equal; to make. that is, the sample he puts in the highest group (call it 11) as much superior to those in the next highest group (call it 10) as the latter are to those he puts in the second from the highest group (call it 9), etc., etc.,—we have in the average [1] result of his groupings his judgment of the relative merits of the samples in a specialty convenient form. For instance, if he grades sample 217 as in group 5 three times, as in group 4 once, and as in group 6 once, and grades sample 218 as in group 6 three times, in group 5 once, and in group 7 once, he judges 218 to be " 1 " better than 217, " 1 " being, in the individual's judgment, one tenth of the difference between group 1 and group 11.
If thirty or forty individuals chosen from competent judges of handwriting thus judge the 1000 samples, the average[1] of all
( 87/5) their gradings give approximately the relative merit of each sample in the judgment of competent judges in general. If they grade sample 317 in group 3 two times, in group 4 five times, in group 5 thirteen times, in group 6 thirteen times, in group 7 five times, and in group 8 two times, their average or median grade for it is 5.5. If their average or median grade for sample 318 is 6.4, they esteem 318 as .9 better than 317. The .9 means, in their judgment, nine tenths of one tenth of the difference between grade one and grade eleven.
If now from all the 1000 samples we could find some which were graded exactly 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 by the average or median[2] judgment of 30 or 40 competent judges, each grading*the set into groups 1 to 11 by what he thinks are equal steps in merit, we would have a very useful scale of merit in handwriting. It would include all grades from the worst to the best and would proceed by what were, by the average competent opinion, equal steps. Or if we could find some graded 1.5, 2.4, 3.3, 4.2. 5. 1, 6.o, 6.9, 7.8. 8.7, 9.6, and 10.5 we would have a scale nearly as useful. It would net be so likely to include the very worst and very best samples, but would proceed by equal steps, as before.
The scale which I shall proceed to describe was obtained by a method in principle the same as the above.
Such a scale could be got in a different way, as follows: Suppose competent judges to compare each sample with every other, stating in each case which was better. If then we picked out samples a, b, c, d, etc., such that a was judged better than b, just as often as b was judged better than c, and just as often as c was judged better than d, and so on, we could have, in samples a, b, c, d, etc., a scale by equal steps, if two other conditions were fulfilled by them. The first of these conditions would be that a should not be' judged better than b and worse than b equally often. For if it were, a would be equal to b, b to c, c to d and so on,' and we .would have no extent to our scale. The second of these conditions would be that a should not always be judged better than b. For, if it were, it might be just enough better to barely be so judged, or it might be very, very much better.
( 88/6) Only if differences are not always noticed can we say that differences equally often noticed are equal. But if we had, as a result of the judgments, facts like those below, we could say that a, b, c, d, etc., represented samples of writing progressing by equal steps of difference in quality.
1000 comparisons of a, b, c, d, etc., being made :
a was judged better than b in 73 per cent., equal to b in 11 per cent., and worse than b in 16 per cent. of the judgments.
b was judged better than c in 73 per cent., equal to c in 11 per cent., and worse than c in 16 per cent. of the judgments.
c was judged better than d in 73 per cent., equal to b in 11 per cent., and worse thanin 16 per cent of the judgments, and so on for d-e, e-f . . . n.
The scale which I shall describe was tested throughout by this second method. The two methods do not give results that correspond exactly. The variations follow this rule: Judges will notice differences between poor samples when they compare them directly one with another which they would not count in rating them by a mental scale. For example, suppose samples a, b, e, and d to be rated 10, 9, 3, and 2 by comparison with a mental scale of eleven grades by equal steps. The percentage of judges regarding to as better than 9 will he smaller than that regarding 3 as better than 2.
Since we get two different scales by the two methods, there are four alternatives. We may adopt one or the other or combine them, or give the results by both methods. I shall take the latter alternative, but shall at this point present only the scale as derived by the first method. In a later section (Section 12) the scale as derived by the second method will be presented.
The scale given here is then a scale in which the steps of difference are equal in the sense of being called equal by competent judges. Equal will mean just this in the next three sections. They are not equal in the sense of being equally often noticed when the single question " better or worse," is answered for each sample in connection with every other sample. The differences in the upper part of the scale would be less often so noticed than those in its lowest third.
( 89/7)
Section 3. The Nature of the Scale
Pages 11 to 37 contain or rather are the scale for merit of the handwriting of children of grades 5 to 8. It is not a scale of merit of the writings of children of grades 1 to 4 or of the writings of boys and girls of the high-school age. It can, however, be more or less well used for such cases until we get more appropriate scales. Each set of samples represents a point on this scale. The samples on page 11 are of quality 18 and 17; the samples on page 13 are of quality 16; the samples on pages 15 and 17 are of quality 15 ; and so on.
The use of 7, 8, 9, 10, II, 12, 13, 14, 15, 16, and 17 for these qualities of handwriting means, first of all, that 14 is as much better than 13, as 13 is than 12; that 13 is as much better than 12, as 12 is than i 1, and so on. In the second place it means that quality 14 is two times as far above 0 merit in handwriting as quality 7 is; that quality 16 is twice as far above o merit in hand-writing as quality 8 is, and so on.. Zero merit is defined roughly as writing as bad as sample 140 (see page 45), as a hand-writing, recognizable as such, but of absolutely no merit as hand-writing. The use of several samples under one quality means that those samples are of equal merit. The scale includes samples of as many different styles is could be obtained, so that in using the scale the merit of any sample of any style of writing can be quickly ascertained by comparison with the scale. The scale extends in actual samples by children from nearly the worst writing [3] of fourth-grade children (quality 5) to nearly the best writing of eighth-grade children (quality 17). Quality 7 is nearly the worst writing of fifth-grade children.
The scale includes a sample of a copy-book model which is rated by competent judges as of approximately quality 18, two samples of fourth-grade writing which are judged to be approximately of qualities 6 and 5, and a very bad writing, artificially produced, which is rated by competent judges as of approximately quality 4. The scale thus extends from a quality, better than which no pupil is expected to produce, down to a quality so bad as to be intolerable, and probably almost never found, in school practice in the grammar grades.
( 90/8)
If one had a finer scale, its use would give but slightly more accurate results, and would require more practice and more time.
Any specimen of handwriting is measured by this scale by putting it alongside the scale, as it were, and seeing to what point on the scale it is nearest. Thus, the sample below (sample 9) is measured by comparing it with pages 11 to 37. I judge it to be between quality 15 and quality 14 and assign it the measure 14 rather than any other unit measure of the scale. If one wishes to .measure more finely than to units, he can add or subtract a fraction according as the sample to be measured seems better or worse than the quality of the scale to which it is nearest.
The sample to be measured should, for convenience, be examined with the entire scale in view. If the scale's samples are arranged in order on a table or against a wall, the examined sample is easily compared with them. 'The measurer then decides what quality of the scale the sample possesses and records the measure. The measurer should be, of course, careful not to decide its grade because of its likeness in style, but only because of its likeness in quality to some sample of the scale. If, for instance, one has a pronounced vertical that is really of quality 7, one must not call it quality 8, because it is in style more like sample 14 than like the sample of quality 7. The measure may be made more and more accurate by having other judges also measure, each always in ignorance of the ratings given by the others. In default of other judges, the measure may, be made more accurate by rating the sample two or more times, each time in ignorance of the ratings previously given. An individual may be measured more accurately by using several samples of his writing, each being rated in ignorance of the ratings given to the other sample.
Section 4 Criticisms of the Scale
The scale has, as previously noted, some defects. First of all, not all styles of writing are represented on the scale, much less at each point of quality on it. For example, we have no pronounced backhand writings of certain qualities and no very pronounced forward slant of certain qualities. There are hardly any markedly angular writings on the scale. This defect can beat any
( 91/9)
 gr1
gr1
( 92/10) blank
( 93/11)

( 94/12) blank
( 95/13)

( 96/14) blank
( 97/15)

( 98/16) blank
( 99/17)
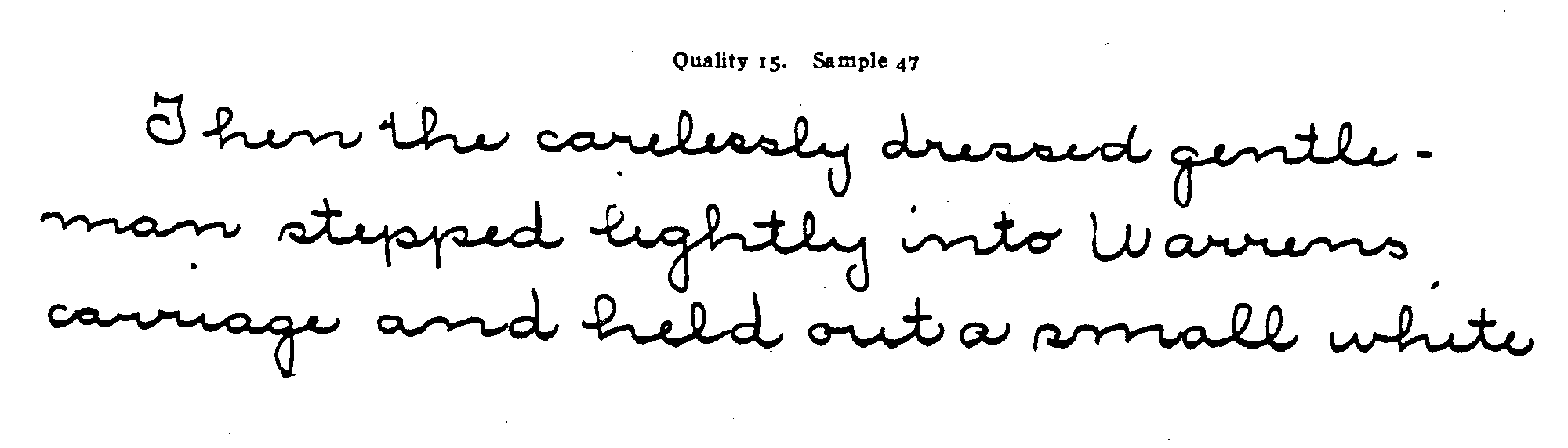
( 100/18) blank
( 101)/19)
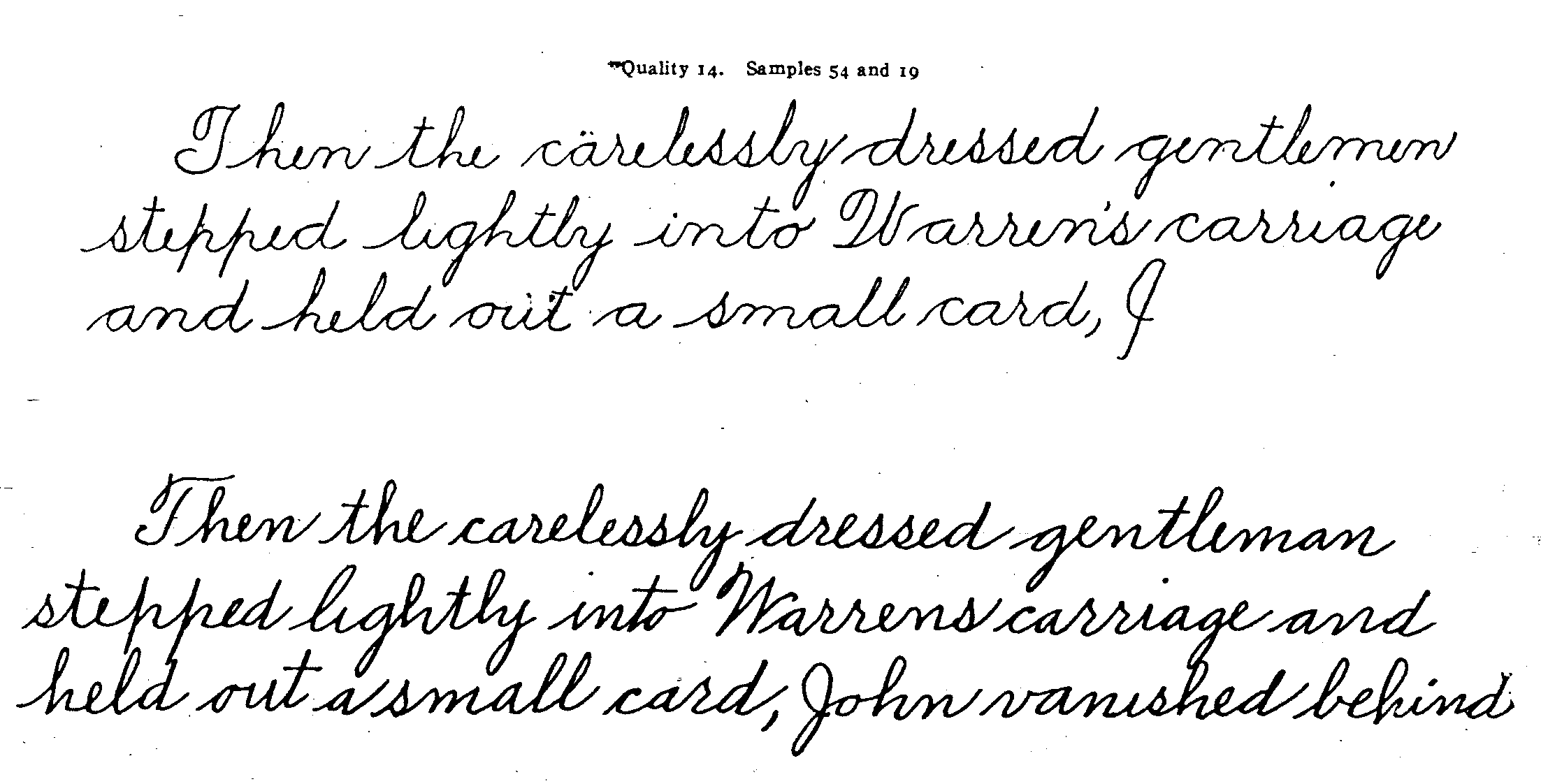
( 102)/20) blank
( 103)/21)

( 104/22) blank
( 105/23)

( 106/24)
( 107/25)

( 108/26) blank
( 109/ 27)

( 110/ 28) blank
( 111/29)

( 112/30) blank
( 113/31)

( 114/32) blank
( 115/33)

( 116/34) blank
( 117/35)
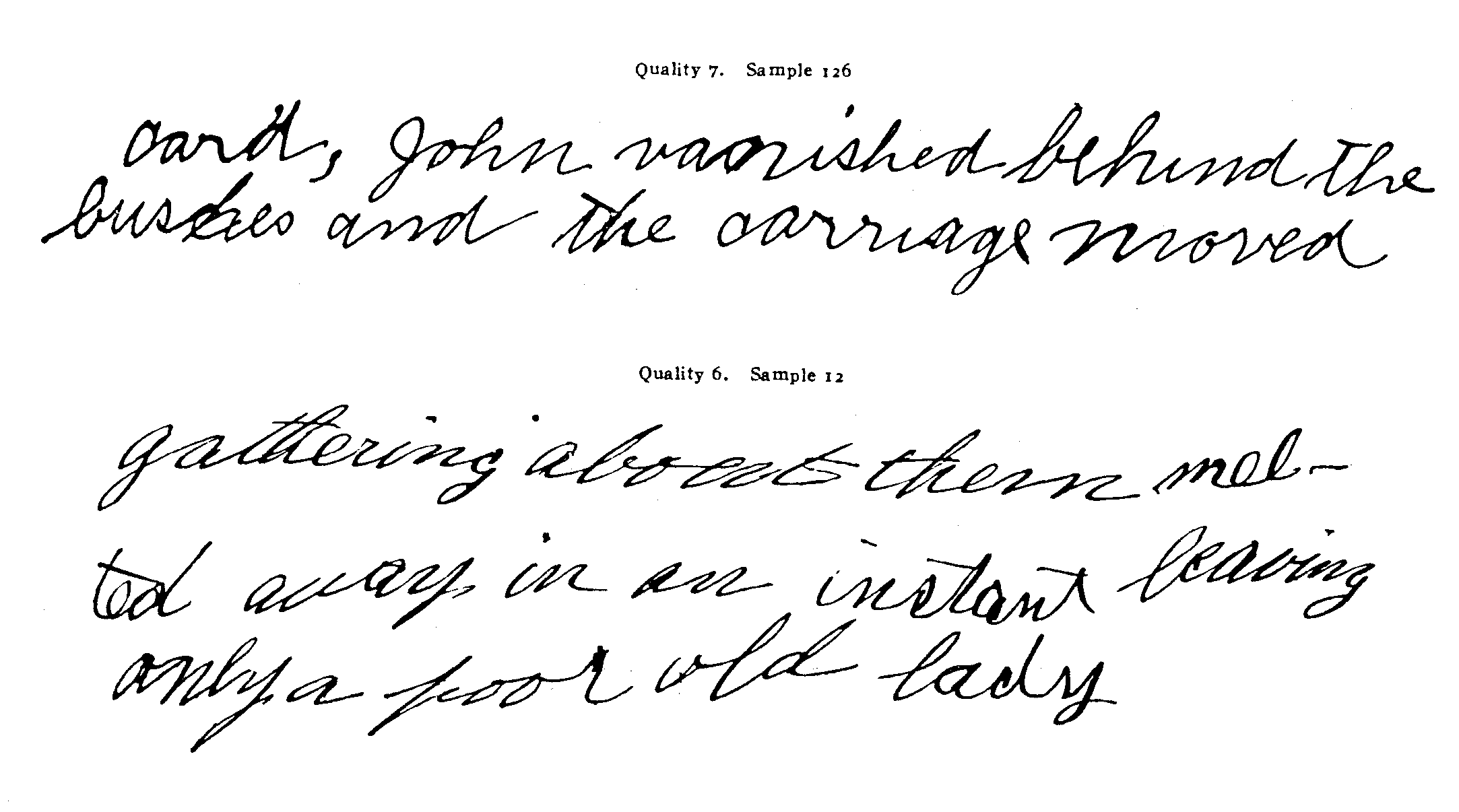
( 118/36) blank
( 119/37)

( 120/38) blank
( 121) time remedied by securing enough samples of children's writing of the missing sorts at approximately the qualities in question, selecting, with the aid of thirty or forty competent judges, samples whose merit is exactly 8 or 10 or 12 or 14 as the case may be, and adding these to the scale. I shall be grateful to any one who sends me collections of children's handwritings of styles not rep-resented in the scale.
Each such sample should be accompanied by a statement of all the grades assigned to it on our scale by at least ten or twelve competent observers, each of whom measures it with the scale and rates it in complete ignorance of the ratings given by all the other judges. It is desirable, though not. necessary, that the writings be on unruled paper.
In the second place, the qualities below 5 and above 17 should perhaps be represented in the scale by 'actual children's writings. This defect could be remedied by collecting 'children's handwritings that were superlatively bad and superlatively good. I shall be grateful to any one who sends me samples of children's writing which are notably better than quality 17 or notably worse than quality 5.
In the third place, although I have so far spoken of the qualities 5, 6, 7, 8, 9, 10, etc., as if they might be absolutely these amounts—as if the 13's might be all absolutely equal in merit and all absolutely halfway between any one of the 12's and any one of the 14's—this is not exactly the case. As was noted on page 3, the scale is only approximate. 16 on the scale does not pretend to mean 16.00000, but between 5.9 and 16.1. 8 does not pretend to mean 8.0, but between 7.9 and 8.1. And as a matter of fact, although I have had a thousand samples graded and have chosen as wisely as I could, some of the samples do vary in merit from 7, 8, 9, 10, etc., by more than .1 plus or minus. Even after one has picked samples that vary only that much, the relations may be altered in the process of making the electrotypes from which the scale is printed or in the process of printing itself. This defect can be remedied by the expenditure of enough time and money in getting more samples, having them graded by more judges, reproducing more of them in electrotypes, and having these reproductions graded again by more judges. In this work I am now engaged. The defect is, however, of little consequence
( 122/ 40) to any use to which any of my readers is likely to put the scale. For the variations in the scale are trivial compared to the variations in individual judgment. I have measured the quality of each sample in the scale to tenths of a step, subject to slight changes had more judges been available and apart from variations in the printing. For example, the quality of sample 49 on page 15 is 15.1, not exactly 15.0.
Similar figures for each sample in the scale are given below. If any one wishes to have the values of each sample as precisely as possible he may substitute these values. In scientific studies of handwriting in schools this should be done, but in practical grading by teachers the 5, 6, 7, 8, etc., of the scale may be kept without the decimal alterations.
What changes might be made in the qualities, if the consensus of thousands of judges were to replace the consensus of from twenty to seventy, is shown in the; figures in the third column, which give the probable average divergences of the former consensus from the latter. They show that the scale is not nearly so precise as, say, a 25 cent scale for weight. But, on the other hand, the superiority of the scale to the personal opinion of any one teacher or investigator is enormous. The latter would have a probable average divergence of from 1.0 to 1.6 from the consensus of a thousand competent judges.
|
TABLE I |
||
|---|---|---|
| Sample | Quality | Probable average divergence of the estimated quality from an estimate by an infinite number of judges. |
| 32 | 16.1 | .14 |
| 84 | 16.2 | .43 |
| 47 | 15.0 | .19 |
| 49 | 15.1 | .18 |
| 89 | 15.0 | ..38 |
| 90 | 15.1 | .35 |
| 19 | 14.0 | .20 |
| 54 | 14.0 | .19 |
| 4 | 12.9 | .20 |
| 24 | 13.1 | .18 |
| 26 | 12.9 | .18 |
| 55 | 13.1 | .21 |
| 30 | 11.9 | .19 |
| 7 | 12.0 | .20 |
| 2 | 12.0 | .23 |
(123/41)
|
|
||
|---|---|---|
| Sample | Quality | Probable average divergence of the estimated quality from an estimate by an infinite number of judges. |
| 23 | 11.0 | .20 |
| 45 | 11.0 | .19 |
| 106 | 11.0 | .28 |
| 17 | 10.2 | .18 |
| 21 | 9.1 | .15 |
| 28 | 8.9 | .15 |
| 31 | 8.9 | .14 |
| 48 | 8.0 | .14 |
| 14 | 8.1 | .19 |
| 126 | 7.0 | .40 |
The reader, in examining the scale, may think that some of the samples called equal are really unequal. If he objects to vertical writing, lie may, for instance, think that sample 55 printed on page 21 is at least one step worse than sample 24. Such criticisms of the scale are, however, really strong arguments in its favor. For such a critic is surely wrong: That he denies the correctness of the average opinion of forty competent judges means simply that his own judgment is partial or crude, and the fact that each individual's judgments of handwriting are thus partial and crude proves that he needs a scale representing the general judgment of competent people to help him to judge and to teach him to eliminate the unfairness in his own future judgments. If no one felt any disagreement with this scale, it would not be so valuable as it is under the condition that many individuals will think it wrong. For those who are unfair to any style of handwriting or who overemphasize beauty in comparison with legibility, or evenness in comparison with " character," or the reverse, can be proved by the scale to be unfair — that is, to diverge from the average judgment of competent people in general. If they are intelligent. they can learn from the scale to correct their bias.
It is possible, however, that some critic may deny the value of the average judgment of competent people in general and declare that though that judgment pronounces two handwritings equal in merit, he knows that they are not equal. Now conceivably he might be right. But the chances are enormously against his being right, and science naturally cannot count his assurance as of more weight than that of any other judge of equal competence.
( 124/42)
Some more sophisticated critic may object, not that he know that this scale is wrong and prefers his own supposed competence to that of forty of his peers, but that no one can know whether this or any such scale is right. For, he will add, any such scale is subjective,[4] representing only what certain individuals think about the merit or value of samples of handwriting. In this there is some truth. There is no value in average opinion as such. The world was as round, when the most competent judges thought it flat, as it is today. If it should some time be proved that evenness of width of line was the sole criterion of real merit in handwriting, the scale would be wrong. But in the case of handwriting the only available criterion of real "merit '' or " quality " or " goodness " is the average judgment of competent people. A hundred years from now merit in handwriting may mean some-thing different from what it now means and a new scale may be
- required. But what it then means will then be determined by the average judgment of competent men and shown in a scale derived just as this one has been derived. What merit does now: mean is precisely the thing measured by this scale. Merit in handwriting in the judgment of competent people today is the composite of qualities, each duly weighted. wherein the samples marked 12 are as much better than the samples marked so as the latter are than those marked 8, etc. The scale measures not some absolute merit, but merit as now defined in the average judgment of forty or more persons chosen at random from the competent. And no other sort of merit is so well fitted to be the basis of a scale.
A far more sagacious criticism than either of these would be that a scale like this for merit in general is less useful than a scale for legibility alone, or for beauty alone, or for " character " alone. or for ease alone. Of course. I admit that such specialized
( 125/43) scales are highly desirable, and I hope that this scale for general merit will stimulate others to the labor of making similar -scales for legibility alone, beauty alone, and so on. But it seems sure that the scale of most importance and usefulness is that fo; general merit. General merit is that for which school 'grades are oftenest given, in respect to which school systems or classes are oftenest compared, and with which other features of a pupil's achievements are oftenest related. Moreover, only after a scale for general merit has been made can one measure the extent to which legibility, beauty, etc., respectively determine general merit.
So much for criticism of the general method of constructing the' scale. I turn now to possible criticisms of the scaling itself.
Some one may ask why 4. 5, 6, 7, 8, etc., are used as the values of the samples on pages 11 to 37 instead of some other equal-step series of numbers such as 1, 2, 3, 4. 5, 6, etc., or 65, 67 ½, 77 ½, 80, etc. The step is made 1 rather than 2 1/2 because one cannot judge samples precisely enough to profit by more than 18 divisions in a scale. Hence the time spent in deciding whether to call a sample measured by the scale 78 or 76 or 77 and in later computing with the large numbers would be largely wasted. The ratio of the highest to the lowest children's writing in the scale is made 17 to 5 (or roughly 3 ½ to 1), instead of 6 to 1 or 13 to 9 (97 ½ to 67 ½) because, from the average opinion of competent judges and the facts of individual differences in motor ability, zeal for handwriting, and other factors determining the quality of a pupil's writing, the best writing from children in these grades seems likely to possess less than six times as much merit as the worst, but more than one and a third times as much—in other words, to be less than six times as far, but more than twice as far, beyond zero merit.
That is, the scale was arranged so that the numbers representing the distances beyond zero of the best and worst samples of children's writing in our scale should stand in the ratio of approximately 3 ½ to 1, and also so that the numbers on the scale should be the smallest compatible with as accurate measurement of handwritings as educational theory and practice need. If any one prefers as a scaling 15, 17, 19, 21... .43. or 3, 4, 5, 6 . . . 17, or 7, 8. 9, 10... .21, it would be hard to prove to him that his choice was inferior to the 4, 5, 6, 7, 8.... 18 used. The
( 126/44) essential thing is that the steps be equal, and that the ratio which the amount attached to the best children's writing bears to the amount attached to the worst be a reasonable one.
Having defined what was meant by 0 merit (see sample 140 on. page 45), I judged as best I could how many times as far there-from sample 141 [5] was than sample 2 [6] was. The judgment of 3 2/5 times is by no means final. Indeed I am now engaged in an investigation aiming to revise it. I could argue plausibly for a ratio as low as 2 ½ to 1 or for one as high as 5 to 1. But a ratio somewhere between 3 to 1 and 3 ½ to 1 seems the 'most reasonable.
The whole matter of the choice of an absolute o for merit in handwriting, and of the consequent absolute values of the points on the scale, is one involving many intricate considerations out of place in this discussion. I fear that in touching upon it at all I may have perplexed some readers. Such may rest confident that in using the 4, 5, 6, 7, 8, 9, 10, 11, 12, etc., of the scale in measuring a sample of handwriting as they would use 4, 5, 6, 7, 8, 9, 10, II, 12, etc., dollars in measuring the value of a book or a jewel or a trunk, they will commit no error of much consequence or, at least, no error so great as they would be likely to commit by measuring it in any other one way.
Another criticism may be that the scale does not guarantee agreement among the observers using it to measure a sample of handwriting. The same sample may, it will be said, be measured by one person as equal in merit to 8, by another as equal to 10, and by still another as equal to 9. This is true, but it is not the fault of the scale. Observers will disagree in their measurements made with the scale, but not nearly so much as in measurements made without it. No scale guarantees absolute agreement. Observers measuring the length of this line ——— to tenths of a millimeter will not agree. But they will agree better than they would if they had no scale and judged its length as a savage might.
( 127/45)

( 128/46)
Section 5. The Use of the Scale
The topic of this section is fitly treated in the one statement: Any measurement of the quality of handwriting may be made more accurately and conveniently with the scale, either actually present or held in memory, than without it. The reader may apply this statement to whatever cases his interests suggest. I shall mention a few of the commoner uses and explain the function of the scale as a standard held in memory.
The class-room teacher has to measure the quality of a single pupil's handwriting in order to assign him a rating in comparison with his fellows and, better still, in comparison with his own past performances. If she uses the scale either by giving its numerical measures outright or by letting her A, B, C's, or 75, 80, 82, etc., per cents, or excellents, goods, fairs, etc., mean certain points on the scale, her ratings will have a definite meaning to the pupil, can have the same meanings that similar ratings by other teachers in the school have, and may be used to measure the actual improvement of the pupil month by month and year by year. She can more easily and more accurately measure the relative values of the different methods of teaching which she may from time to time employ, of different lengths of periods for drill, and the like.
A principal or supervisor or superintendent of schools needs to measure the quality of the handwriting of individuals, of classes, and of all classes of the same grade, in a school or system. If he has such measures honestly made by the scale, he can compare the work of one teacher with that of another, the work within his own school or city with that of other schools or cities and with that of his own city five years later. the work of schools using one system of writing with that of schools using other systems, and the like. If he tried without the scale to estimate the superiority or inferiority in handwriting of twelve-year-olds in city A to twelve-year-olds in city B, he would have to collect - many samples in both cities and have them graded alike. He could define the amount of difference found only by actually exhibiting it in samples or by making out a scale like ours, defining it as I have done, and expressing the difference as such a distance on the scale. With the scale in use in both cities, on the con-
( 129/47) -trary, if marks are honestly given by the teachers, the superiority or inferiority of any group will be measured by the difference in the scale-values of the marks themselves.
The scientific student of education will use the scale to measure the quality of samples of handwriting from individuals, classes, cities, groups chosen for grade, age, sex, method of teaching, or length of time devoted to writing, and from any other sources. He will also be able to use any marks or ratings honestly given by teachers or others.
Whoever has any occasion to define a standard of quality in handwriting can define it unmistakably and conveniently by the scale. Business men can decide what quality they wish the schools to secure in the boy fourteen years old who is to apply for clerical positions. A supervisor can inform all the teachers of say, grade 7 that the minimum requirement is, say, quality 11, at a rate of 50 letters per minute, that the average pupil must be made to write at quality 13 at a rate of 60 letters per minute, and so on. Whatever standard is set will be absolutely defined by those who set it and will be clear to all those who are to follow it.
The pupil himself may profitably know and use the scale. He may see by it what is expected of him and may tell how nearly he reaches the standard and how much he has gained.
Even if precision is not desired in the estimate of the quality of handwriting, — even if good and bad or satisfactory and unsatisfactory are the only ratings to be given,— the scale is none the less useful. For if good and bad, or satisfactory and unsatisfactory are to mean anything, they must mean handwritings above. and below some point on some scale of merit. They can be properly defined only by locating that point. And until some better scale is available that point can be located only by exhibiting samples or by stating the numerical value these samples would have on our scale.
To put the whole matter in a word, any measurement of the quality of handwriting should be 'made by the scale and reported in terms of the scale, for substantially the same reasons that any measurement of the length of an object should be made with a linear scale and reported in meters or feet.
( 130/48)
Measurements may be made by the scale without the comparison of the sample with the actual scale itself. just, as one uses his experience of feet and inches as a mental standard whereby he estimates more or less accurately the length of pencils, tables, windows, and the like, without an actual ruler or tape, so one may come to estimate that this sample of writing is about quality 16, that one about quality 9, and the like, from the mental standard left from examination and use of the actual scale. The scale should always be present for reference in any measurement which requires exactitude, but it will do its greatest amount of service, not by actually serving as a foot-rule for quality in hand-writing, but by creating in the minds of teachers mental standards to be used in even the most casual ratings of everyday school-room life. To one who uses the scale quality 18 or quality 15 or quality 7 comes to be a definite agent in determining all judgments, just as 18 inches or 15 pounds or 7 dollars is. just as a child learns to think about length correctly and with fair precision without a ruler in his hand by having measured off lengths with it, so teachers may come to think about handwriting correctly and with fair precision without the scale before their eyes, by having measured handwritings with it. just as the thermometer teaches us to supplant the vague " very cold,"" cold,"" moderate,"" warm;'' " hot," and " very hot " by " about o," " about freezing,"" about 60 degrees,"" about 7o degrees,"" about 80 degrees,"" nearly 100," and the like, so the graphometer can teach us to supplant the vague " illegible,"" very hard to read," " a good plain hand," and the like, by judgments which mean something definite and constant to those who make and those who hear them.
Section 6. A Scale for Quality in Adult Women's Handwriting
The scale for adult women's handwriting consists of only six points, each represented by only one sample. Let us call these samples a, b, c, d, e, and f. They represent the best selection that I could make of writings ranging from nearly the best to nearly the worst of the ordinary writing of some five hundred women teachers and students and differing progressively by
( 131/49) equal degrees of merit. The derivation of the scale was as follows:
Thirty judges rated samples a, b, c, d, e, and f together with from 37 to 456 other samples. - The ratings given were from 1 (the lowest grade) to 11 (the highest), grades 1 and 11 being roughly shown by samples and the requirements being made that the grades 2, 3, 4, 5, etc., should represent grades of merit differing by equal steps. The number of the samples was reduced from 456 to 37 by gradually dropping samples which seemed unlikely to be near the points 1 to 11. The result of the thirty ratings was as shown in Table II.
| Quality | Frequencies of Each Quality for Each Sample | |||||
|---|---|---|---|---|---|---|
| a | b | c | d | e | f | |
| 1 | 20 | 1 | 1 | |||
| 2 | 7 | 12 | ||||
| 3 | 1 | 6 | 2 | 1 | ||
| 4 | 2 | 6 | 7 | 1 | ||
| 5 | 2 | 10 | 6 | 1 | ||
| 6 | 1 | 5 | 3 | 2 | ||
| 7 | 3 | 8 | 6 | 2 | ||
| 8 | 1 | 1 | 3 | 4 | ||
| 9 | 1 | 5 | 6 | 3 | ||
| 10 | 1 | 6 | 6 | |||
| 11 | 3 | 5 | 19 | |||
Bearing in mind that a rating of quality 1 means 1 or worse than 1 and that a rating of quality 11 means 11 or better than 11, it is clear that in the combined judgment of all 30 judges a, b, c, d, a and f represent qualities progressing by approximately equal steps. Thus 10 of the judges ranked a as better than 1, 10 ranked b as better than 3, and 0 ranked c as better than 5, 12 ranked d as better than 7, and 11 ranked a as better than 9. Of the 20 judgments of a as 1, it is probable that about 10 would have been " worse than 1 " had the series included a lower range. Of the 18 judgments of f as 11 , it is probable that about 10 would have been "better than it " had the series included a higher range. The median values of a, b, c, etc., with this interpretation of the grades 1 and 11, are: 1.0, 2.833. 5.0. 7.125, 8.833
( 132/50) and 10.94, the differences in quality being respectively 1.833, 2.167, 2.125, 10001.708, and 2.107.
These six samples were then printed and were graded in their printed form, together with seven other samples of approximately the qualities 1, 3, 5, 5, 7, 9 and 11, by thirty-eight judges. The ratings in this case were in 6 grades, to progress by equal steps. These were called by the judges 1, 2, 10003, 4, 5 and 6, but represent respectively 1, 3, 5, 7, 9 and 11 of the gradings just presented, in Table II. Hence in Table III, which gives the results of the gradings by these thirty-eight judges, I shall use 1, 3, 5, etc. for 1, 2, 3, etc.
|
Quality |
Frequencies of Each Quality for Each Sample |
|||||
|---|---|---|---|---|---|---|
| a | b* | c | d | e | f | |
| 1 | 32 | 7 | ||||
| 3 | 5 | 21 | 8 | 3 | ||
| 5 | 1 | 9 | 19 | 12 | 1 | |
| 7 | 9 | 19 | 6 | 3 | ||
| 9 | 2 | 3 | 22 | 13 | ||
| 11 | 1 | 9 | 22 | |||
* only 37 judges rated this sample.
The median ratings for a, b, c, etc., are .8, 3.1, 5.1, 6.4, 9.1, 10.7.
These thirteen printed samples were then rated together with from 58 to 104 samples of children's handwriting, including samples much better than the best 0f the adults', by 26 judges. The ratings were from I to 11, but the meanings of these numbers were unlike those attached to them in Tables II and III, except in the case of the I. The 3, 5, 7, 9, and 11 of Tables II and III have approximately the values 2.4, 3.8, 5.2, 6.6, and 8. Finally, the thirteen samples were rated, together with 120 1000sampies of children's writings, including some still better and some still worse, by 9 judges. The ratings were 0 t0 12 1000but the values of the 1, 3, 5, 7, 9, and 11 1000of Tables II and III were, as before, approximately 1, 2.4, 3.8, 5.2, 6.6 and 8. The median values attached by the 35 judges were, for a, b, c, d, e, and f, in order, 1, 2.4, 3.83, 5.3, 6.5, and 7.9.
We have then as a result of the three series of judgments, numbering 103 in all, the following:
( 133/ 51)
Differences between a and b, b and c, c and d,: etc.:
I. Using the median ratings of 30 judges (ink samples) : 1.83, 2.17, 2.13, 1.71, 2.11.
II. Using the median ratings of 38 judges (print) : 2.3, 2.0, 1.3, 2.7, 1.6.
III. Using the median ratings of 35 judges (print, long series) reduced to equivalences with (I) and (II): 2.0, 2.04, 2.1, 1.7, 2.0.
Average differences : a-b, 2.04; b-c, 2.07; c-d, 1.84; d-e, 2.04; e-f, 1.91.
The approximate equality of the steps may. be verified by ascertaining how often b is rated higher than a, how often c is rated higher than b, etc., that is, by an adaptation of the so-called method of right and wrong cases. The facts are as follows :
| Long series written samples |
Series of 13 printed samples |
Series of 71 to 133 printed samples |
All series together |
|
|---|---|---|---|---|
| No of Comparisons | 30 | 37 | 35 | 102 |
| b rated as better than a | 25* | 26 | 23 | 74 |
| c rated as better than b | 26* | 25* | 27* | 78 |
| d rated as better than c | 23 | 25* | 27* | 73 |
| e rated as better than d | 23 | 29 | 19 | 71 |
| f rated as better than e | 23* | 24 | 26 | 73 |
In the starred cases the obtained figure was 1 less than that printed, but from a number of comparisons it was also 1 less than that printed at the top of the column.
Samples a, b, c, d, e, and f thus represent points on a scale of quality differing each from the next by approximately equal steps. We can properly call their values in order x, x+2, x+4, x+6, x+8, and x+10 where 1.0 equals a difference roughly equal to one-tenth of the difference between the best ten and the worst ten of a thousand samples each from an adult woman student, and x equals the average quality of the worst ten of the thousand. To be more precise we should call them, in order, x, x+2.0, x+4.1, x+6.0, x+8.0, and x+9.9.
( 134/52)
To turn these values into numbers referring to zero merit as a starting point we must define zero merit for adult handwriting and measure the distance of x from it.
This I have not attempted to do at all adequately since the need of an elaborate scale is not nearly so great in the case of adult handwriting as in the case of children's writing. Quality x of the adult scale is judged by the average of some forty individuals to be approximately equal to quality 8 of the children's scale. A difference of 1.0 along the adult scale is judged to be approximately equal to a difference of .7 along the children's scale. If we take the zero point for adults as approximately the same as for children of grades 5, 6, 7, and 8, the qualities of a, b, c, etc., may be taken as approximately equal, in order, to 8, 9.4, 10.8, 12.3, 13.6, and 14.9 or 15 on an absolute scale whose zero is a writing recognizable as an attempt to write, but of zero merit. Such a numbering would not be far wrong.
This adult scale very much needs samples of other styles at each point. Perhaps I should have delayed printing it until such had been obtained, but the labor and expense of collecting and selecting, by grading and gradual elimination, samples to fit exactly certain points on the scale is very great. The present scale has required thousands of gradings. It will be of great value in economizing the time and money of any one who wishes to make a better scale, if in no other way.
As a matter of fact, in spite of its lack of samples of all styles at each point, it will also be of service in every case where the quality of a woman's handwriting is to be definitely known.
For example, (1) the authorities of a college or a normal school wish to set a clear standard as to how good handwriting must be in order to make an examination paper, or a composition, or other written work, acceptable. If they set this standard as "at least as good as quality c of the Thorndike scale " every student, every member of the teaching staff, the faculties of other colleges, and the public can tell just what the standard is. There can be real as well as " paper " uniformity in the standard.
(2) In civil service examinations, examinations for teacher's licenses and the like, the standard of a certain quality by the scale at a certain minimum speed can be set and the candidates can
( 135/53)

( 136/54) blank
( 137 / 55)

( 138 / 56) blank
( 139/ 57)
( 140 / 58) blank
( 141 / 59)

( 142 / 60) blank
( 143 / 61)

( 144 / 62)
( 145 / 63)

( 146/ 64) blank
( 147 / 65) be exactly, impartially, and uniformly (all over the country, if desired) rated.
(3) The relation between (a) ability 1000in handwriting 1000under the pressure of school drill to (b) ability in handwriting in later life requires for study some adult scale'. So also with any 1000other relation of the quality of adult handwriting to anything.
I shall be indebted to any one who will send me samples of adult women's
handwriting, especially of vertical writing of qualities d, c, b, a, and worse;
of pronounced slant writing of qualities d, e; f, and better, and of pronounced
backhand writing of all qualities. Each such sample should be accompanied by a
statement of all the grades assigned to it on our scale by ten or twelve
competent observers, each of whom judges in entire ignorance of the judgments
made by all. the others. It is desirable, though not necessary, that the
.writings be on unruled paper.
Sections 7. The Derivation of the Scales [7]
Certain partial descriptions of the means and methods by which the children's scale and adult women's scale were derived have been 'given in sections 2 .and 6. A full account of the derivation of either is inadvisable both because it would necessarily be extremely long and because much of the work done was such as I now know, from the very experience of doing it and seeing its results, to have been unnecessary.
I shall therefore give only such notes as are likely to be helpful to any one who is stimulated by this scale to construct similar scales for other educational products.
To construct a scale by which to measure various qualities (that is, amounts of merit) in handwriting ranging from, say, x to x +y, it is desirable to have samples of qualities, not only of every degree from x to x + y, but also of qualities worse than x and of qualities better than x + y. The reason is that otherwise the exact values of samples at x or x plus a slight amount and of samples at x + y or x + y minus a slight amount cannot be directly measured, but only inferred.
( 148/66)
For example, call x 1 and y 10. X+y then being 11, x or 1 is nearly the worst and x+y or 11 "is nearly the best of a series of samples, ranging continuously from x to x + y.
If now any one is required to fix in mind 11 points including x (or 1) and x + y (or 11) differing each from the next by equal amounts, and to rate each of the samples as 1, 2, 3, 9, 10, or 11, according to which of these mentally fixed points it seems most like, he can err by rating a sample as 2 or 3 when it is really 1, but cannot err by rating it 0 or minus 1 when it is really 1. Similarly he can err by rating it 9 or 10 when it is really 11, but cannot err by rating it 12 or 13. For a sample really close to point 11, rated in the way just described by 33 judges, the results were:
Rated as 11 by 21 judges
Rated as 12 by 7 judges
Rated as 9 by 3 judges
Rated as 8 by 1 judge
Rated as 7 by 1 judge.
The apparent average rating would then be 10.4 and the apparent median rating 10.7. When, however, the samples are increased by some of the real quality x + y + 1 (or 12) and the ratings are to be made at twelve points including x + y + 1 (or 12), a certain proportion of the judges rank the sample in question 12 and the average-and median are raised to nearly 11.
Unless the set of samples to be rated includes some samples, one, two, three, and even four grades better than the best quality (x+ y) to be represented in the final scale and also some samples one, two; and three grades worse than the worst quality (x) to be represented in the final scale, one cannot get the values of x + y and x themselves save by inference.
Hence, to make a scale for the handwritings of, say, 10-year-old school children conveniently, it is necessary to have a collection of-samples varying in quality from much below the worst to much above the best of their writings. This involves the use of " unnatural" samples, which may seem very objectionable, but which as a matter of fact does little or no harm.
In the case of a scale for the merit of English compositions by high-school pupils one should start from a collection of com-
( 149/67) -positions ranging by small gradations from compositions much worse than the worse point on the final scale is to be, to compositions much better than the best point on the final scale is to be. Here the extremely bad ones may be obtained by artificial construction, from the feeble-minded, or from very old and stupid grammar-school children. The extremely good ones may be obtained from the printed or manuscript compositions in youth by gifted authors.
To get samples exactly situated at points differing progressively by equal steps requires that the original set range from one extreme to the other by very slight gradations. This means for practical purposes that one must have at the start a very large number of samples. After these have been graded by enough judges to rate each roughly, only those which are near the points to be represented by the scale need be graded further. As the value of each sample of this narrower .selection is determined more exactly by further judgments, only those very near the points to be represented on the final scale need be preserved for still further judgments ; and so on till the values of enough samples are determined to the degree of precision required for the scale itself.
Points on the scale exactly determined, but not at progressively equal steps, can be got with far less labor. If, for example, after a single rating I had picked samples at intervals from the best to the worst and then had only these few samples rated by the twenty to seventy judges, the value of each could have been stated nearly as exactly as is the case in the samples of the scale. But they would form a series like 17.33, 16.65, 16.28, 15.82, 15.40.15.47, 15.23, 14.95, 14.7, etc.; instead of the approximate 17, 16, 15, 15, 15, 15. 15, 14. 13, 13, 13, etc., of the scale. They would have served the purpose of a scale as well so far as aiding an observer to make exact measurements which any other observer could verify, and to report them unambiguously, but the labor of allowing for the decimal values or of computing measures ex-pressed in awkwardly long numbers would burden each person using the scale'. If the scale were designed for use only by scientific investigators of education, I should have economized in respect to the number of samples rated, had far more ratings of each sample, and presented a scale of very exactly determined
( 150/68) qualities but at irregular intervals. For the common use of pupils, teachers, and supervisory officers a less precise scale by approximately equal steps seemed far more valuable. Also the precise evaluation of each sample can be determined by many students each spending independently a little effort in getting the samples which I print rated : whereas the selection of samples varying by equal steps can be managed best under one individual's supervision.
It is possible that the determination of the amount of difference between two samples by the percentage of judges noticing the difference is preferable to the determination by the amount of difference between their median values as given by judges attempting to apply to each a scale of mentally equal differences. I used both methods. Experience of their use provides many facts of importance to methods of quantitative work in both psychology and education, but the facts would be of interest to only the small proportion of readers to whom surfaces of frequency of errors in judgment are familiar and esteemed friends.
In general, the experience in constructing this scale gives great encouragement to the hope that for many educational facts, units and scales may be invented that shall enable us to think quantitatively in somewhat the same way that we can about facts of physics, chemistry or economics. It has been commonly supposed that the great complexity of such facts as examination papers in spelling, manifestations of interest in history, acts of moral significance, habits of industry, essays, poems, inventions, replies to questions demanding logical inferences, and other like results of education, prevents the samples composing any one such group from being measured by any one linear scale at all comparable to a foot rule or thermometer or galvanometer.
It is true that some judges find it hard to judge handwriting for the complex of legibility, beauty, ease, " character." etc., into which " quality " or " goodness " or “merit " resolves itself. But none of them found it impossible to do so, and most of them rated the writing for the complex, —" merit or goodness in your opinion,"— as readily as an appraiser would rank articles of sale by money price, or as a little child would arrange pieces of paper in the order of their size regardless of the fact that some were squares, some circles and some triangles.
( 151/69)
The entire history of the judgments of the merit of handwritings supports the
claim that if a number of facts are known to vary in the amount of any thing
which can be thought of, they can be measured in respect to it. Otherwise, I may
add, we would not know that they varied in it. Wherever we now properly use any
comparative, we can by ingenuity learn to use defined points on a scale.