Socialization, Logical Reasoning, and Concept Development in the Child
Anselm Strauss and Karl Schuessler
Indiana University
This is a second paper dealing with the development of children's concepts of money. In the first paper a group of business-class children was discussed.[1] Evidence showed that both boys and girls consistently pass through stages of learning, and that each stage is based upon knowledge characteristic of previous stages. Descriptions of behavior at each level were given, and certain limits which age places upon the attainment of levels were noted. In the present paper emphasis is on the following points:
(1) The performances of a group of working-class children (Fairview School) and those of the business-class group (University School)[2] are substantially the same. This suggests that in regard to certain simpler elements of perceiving and role playing there are no important social class differences.
(2) Methodological problems involved in the application of scale analysis to a complex concept, such as money, are considered in further detail.
(3) Detailed consideration is given to the problems of whether conceptual development is cumulative, and whether to reach any given developmental stage the child must have passed through all preceding and simpler stages. If we are to understand socialization in children, viewed partially as conceptual learning, the delineation of consecutive stages is at least a preliminary task.
(4) Stages of conceptual development were previously interpreted by means of such terms as simple-complex, concrete-abstract, rigid-flexible, egocentric-relativistic. This interpretation is supplemented by an analysis
STAGES OF CONCEPTUAL DEVELOPMENT
A main hypothesis tested in this study was that a child's concept of money developsin a consistent and cumulative manner. As in the previous study, three simple aspects of this concept were singled out for investigation: coin recognition (naming coins by various criteria) ; comparative value (which money is worth more) ; and equivalence (making change) .[3] Three schedules were employed to bring out features of concept development, and the scalogram was used to determine whether this development was cumulative.
Scaling and Class Differences. Like the business-class, the responses of the working-class children to each of the three schedules formed a scale, as judged by the reproducibility coefficients, all of which exceeded 90 per cent.[4] This means that from a child's rank order in the group it is possible to predict with at least 90 per cent accuracy his response to every item in the schedule.
The degree of reproducibility for each of the three tests was about the same for both school groups. However, the number of scale
(515)
types for each test was slightly different. These differences result from a difference in the number and position of cutting points in the score arrays; which difference in turn is probably a consequence of sampling errors. For example, the maximum number of scale types [5] will not be reached if one response category has a zero frequency, since in that case the number of cutting points is reduced by one. It was for this reason that on the test of comparative value the Fairview group fell short of the maximum by one, hence had one less type than the University group who reached the maximum. No Fairview child gave the "best" answer to the fifth item: evidently, this item had no differentiating value for this school group. The number of scale types will also fall short of the maxi-mum if the cutting points for two or more items fall at the same place in the array. On the test of recognition the University group fell short of the maximum 11 by 2 because three cutting points fell at the same point in the array, automatically resulting in the loss of two scale types.
Also, scale types unique to each school group occur at the same rank in the array and have small frequencies. Scale types with small frequencies are unstable since by moving the cutting point one or two places in either direction the results of the scale analysis can be changed, although not significantly. By moving the cutting point down one place on Item 5, Test 1, an additional scale type for the University group is created, reducing the discrepancies between the two school groups by one.
The foregoing analysis supports the view expressed above that differences between scalograms for the two social class groups are a sampling effect. Minor differences in the number, composition and rank order of the scale types would undoubtedly diminish, if not vanish, if comparisons were made between large samples. From our standpoint the striking feature of the comparison is not the differences, which may be reasonably ascribed to sampling fluctuations, but the very similar progression of both groups.
The middle- and lower-class children were also contrasted in regard to mean test scores, with age controlled by matching. Mean scores on equivalence and comparative value were not significantly different; but the difference between mean scores on recognition was significant at the 1 per cent level. Since the scale types of both groups on recognition were almost identical, as noted above, the difference between means necessarily is due to a difference in relative frequency with which each type occurred for the two groups.
Inasmuch as there were no major differences between the developmental patterns of the two groups of children, it was advantageous to scale their responses together. When this was done the three topics scaled by the criterion of 90 per cent reproducibility These results rather than the separate scalograms are used in the following discussions, since they have more stability and show better the distinctive features of each scale type---such as relative frequency, characteristic error, organization of response, and median age. This material is presented in Tables 1 and 2.[6]
Sex and Age Differences. In the lives of American men and women, monetary matters are differently emphasized; for instance the adult male does most of the investing while his wife is more likely to be expert at finding bargains. However, whenever there is no difference between the behavior of males and females, one could contend that these facets of their activities fall outside the sex roles. This appears to be so with the behavior covered by our tests. Though one might expect that boys and girls would differ somewhat in their conceptions of money, there are no significant differences between sexes concerning the rather simple knowledge of money involved in recognizing

(516) coins coins and in being able to find equivalences and comparative values. Like the University children, Fairview boys and girls, matched by age, were similar in their performances as judged by the results of the t test: no t value reached the 5 per cent level of significance.
A high correlation between chronological age and performance was found for business-class children. Fairview results are about the same.[7]
Also the same limitations placed by age upon level of conceptual development are
(517)
 found again in the Fairview data. These limitations can be seen from Tables 1
and 2 where median age and range are given for each scale type. Statements about
the earliest age at which a child can be expected to fall into a given scale
type cannot be made with great certainty because of limited sampling;
nevertheless the figures strongly suggest that definite limitations are placed
upon acquisition of monetary concepts by the factors subsumed under the general
term "age,"
found again in the Fairview data. These limitations can be seen from Tables 1
and 2 where median age and range are given for each scale type. Statements about
the earliest age at which a child can be expected to fall into a given scale
type cannot be made with great certainty because of limited sampling;
nevertheless the figures strongly suggest that definite limitations are placed
upon acquisition of monetary concepts by the factors subsumed under the general
term "age,"
Perception and error. In recent years the topics of perception and error have beentreated largely in terms of "need" and "interest." By way of contrast, we wish to emphasize the point, not that need and interest are unrelated to perceiving, but that they affect perception only after concepts are learned. That is, the complex perceptions of the adult rest upon his possession of certain complex concepts. Before the child acquires these concepts, his perceptions are relatively undifferentiated.
Tables 1 and 2 bear upon this point. Specifically, they support the hypotheses that (a) perception is organized around concepts and (b) that error is in part due to the
(518) subject's conceptual deficiencies.[8] At each stage of development, the child exhibits blindness and commits errors because he has not yet grasped necessary conceptual distinctions. A detailed and lengthy analysis of error could be made but we shall confine ourselves to a few illustrations.
A child may have learned to perceive-i.e., to distinguish between-the various coins, but he may not yet perceive that these coins have writings on them, or may consider these writings irrelevant. The inscriptions may also lead him into what the adult would consider contradictory positions. One child stoutly maintained that a Canadian penny was not a penny when the maple leaf was showing but that it was a penny when the head was face up. The child may see two nickels not as members of a single class in the logical sense-and therefore interchangeable-but consider them as two different objects. One is his own, and the other is someone else's, and they cannot be substituted one for the other. In sociological terms, he has a sacred attitude toward his own nickel rather than a secular.
The child may make errors of addition as well as omission. Thus at the time when they learn that a nickel "is five cents," but as yet have no concepts of these classes in the adult sense, the children sometimes believe the nickel actually contains the pennies. If you were to open up the nickel, you would find the pennies therein-sometimes brown, sometimes white.
A little knowledge can be dangerous: whereas some children choose as more valuable any pile containing a large coin, some children who have become sophisticated about number choose, say, two nickels and a dime over a penny and a fifty-cent piece "because this one has three and that one has two." Similarly, whereas very young children ignore inscriptions and so think Canadian nickels are just nickels, older children who cannot yet read the number inscription but who notice the figures will balk when confronted with the Canadian nickel, which has a beaver on it.
The very youngest children fail to match exactly the investigator's coins when told to do so, for they see merely that he has put forth some things, or they see a number of coins rather than specific coins. The investigator, also, may show children of all ages who fail to make change abstractly how to do so. The child may say he understands (i.e., "sees"). Actually he often does not, since his imitation proves to be faulty.
Interesting cases of reversion or confusion sometimes occur. Thus one child took the Portuguese ten-centavos coin for a penny, because it is brown. When the 10 was pointed out to him, he decided immediately that it was a dime. Later, in the test of equivalence, the investigator included this coin with the others, leaving the 10 clearly in view. The child then sometimes treated it as a penny and sometimes as a dime. Similarly, a child was supposed to match the investigator's thirty cents, and the only way he could do this was to give from his own pile five pennies, three nickels, and a dime. After several trials he announced that it could not be done. The reason it could not be done was that the child treated all the pennies in his pile (nine) as a single unbreakable unit instead of regarding each as separate. In logical terminology, he did not treat each penny as a class representative, equal and equivalent to every other representative-something he was previously able to do when encountering simpler problems, and was still able to do when his mistake was pointed out.
ASSOCIATION
To determine how conceptual development in one area was related to development in the other two, (a) correlations between test scores were computed and (b) association between specific items on tests was gauged by X2. The correlation coefficients indicated that general levels of conceptual development are
(519) directly related. This had been previously established for the University group.[9]
To measure association between specific items in different tests, responses were arranged in contingency tables and X2 values computed when possible. This detailed analysis confirmed what had been anticipated from the correlation results. The least amount of association, judged by the relative number of times x2 reached the 1 per cent level of significance, was between recognition and evaluation; the association was about equal between recognition-equivalence and evaluation-equivalence. Further, this statistical material shows that, for any pair of items, success tends to be related to success. An important exception, brought out by the contingency table, is that while success on a simple item can be predicted from success on a difficult one, the reverse is not true.
Those especially interested in scale analysis may ask whether scaling was used to study the independence of the three dimensions (recognition, evaluation, and equivalence). The notion that more than one variable is being measured if the items do not scale is applicable in this connection. But this rule has a serious limitation: if the items do not scale, then more than one variable is involved; but if the items scale, it does not follow that only one variable is involved.
For whatever suggestiveness they might have, we present the results of scaling the tests two at a time. The reproducibility coefficients dropped slightly below 90 per cent for each scalogram—an insignificant drop.[10] This evidence may be interpreted in
one of two ways: (a) only one dimension is involved rather than three, or (b) dimensions are separate and distinct but nevertheless scale together. An example may help to clarify the latter interpretation, which is the one we favor. Latin and Mathematics items may form a scale but no one would claim that therefore Mathematics is Latin; neither does the fact that both are perfectly correlated with a common factor make them identical.
ITEMS RANKED BY DIFFICULTY
To determine which responses on all three tests are necessary prerequisites to other responses, a rank order of all items by difficulty was worked out. Items were arranged in a single scalogram and cutting points determined for each item. The number of scores above the first cutting point was then used as the criterion of difficulty. When first cutting points coincided, second cutting points were employed to differentiate items by relative difficulty. The rank order of items established by this method is shown in Table 3.
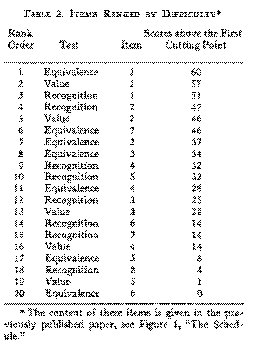
(520)
Items are considered equal in difficulty if the number of cases or scores above the first cutting point does not differ by more than five.[11] The scalogram method allows the interpretation that to pass a certain item a person must have passed all items ranked in terms of difficulty as less than, or equal to, that item. This interpretation can be made only if the items form a scale.[12] Our data can be interpreted in this way as the scalogram for all three tests combined had a reproducibility coefficient of .87.
Ranking by scalogram has distinct ad-vantages over the chief method now in use for the study of conceptual development in children. This latter method determines what children at a given age know "on the aver-age" about a certain topic such as time, number, death, or social class.[13] Conclusions consist of statements like "at a given age the child knows this, and at another age he also knows that." This procedure fails to indicate how many children passed a more difficult item while failing an easier one, although most children of given ages who pass a difficult item also passed the easier ones.
Ranking by scalogram also makes possible the addition of items which represent Other aspects of the concept money. The relative difficulty of these items, as well as their relationships with all other items, can be determined. The outcome of such analysis then can be used to make increasingly de-tailed statements about developmental stages and their prerequisites. This procedure is especially fruitful since in this way conditions necessary to any stage of development for "money"-or probably any concept- can be studied.[14]
Another difficulty with the customary method is that it reveals only in a rather vague way that one item is both more difficult than another and is learned later. This difficulty has been met in at least two ways. (a) a single concept was broken down into a few of its many component aspects and their relationships shown, and (b) the use of logical notation revealed the logical operations implicit in the children's responses to each item as well as clarifying the connections between these operations (as will be shown in the next section).
CONCEPT FORMATION AND LOGICAL REASONING
An argument popular with child psychologists is that "the child's reasoning processes at the age of six are [not] essentially different from his reasoning processes at the age of twelve or eighteen."[15] This argument involves the following points. First, children's logic is "essentially" the same as adults'. Second, the more frequent errors committed by the child are a con-
(521) -sequence of false premises rather than of inferior logic or inability to reason abstractly. Third, these false premises are the result of inadequate "experience" with the given subject matter. Fourth, adults-like children-when confronted by unfamiliar subject matter are likely to commit errors in logic and judgment. The view that children must have certain requisite experiences is an efficient explanation of why they can-not be forced before their time to master certain concepts.
This argument is fully as important for social psychologists as it is for child psychologists. For if, actually, children do not reason "essentially" the same as adults then a peculiarly subtle kind of anthropomorphizing of the child is being committed by many investigators. It is virtually a canon in social psychology that we must not at-tribute to children the perceptual and mental sophistication that is granted to most adults, nevertheless a considerable number of personality theorists attribute substantially the same sort of perception, motives, and rationales to children as to adults.
Our study, although confined to a. limited topic, supports the opposite hypothesis that significant differences in logical reasoning among children of different ages exist. In Tests 2 and 3 certain items cannot be passed unless certain logical operations were previously mastered.[16] For purposes of brevity only certain items from Test 3 will be discussed although the conclusions cited apply equally to the remaining items and to all of Test 2.
The order of items in Test 3 by difficulty can be seen from Table 3. Table 4 [17] gives excerpts from three items and the logical operations involved in passing each item. These three particular items were selected because they are, respectively, next to the easiest, the middle, and next to the most difficult items. (The easiest item, I, involves mere sensorimotor matching of coins by color and size, not logical relation; while the most difficult, 6, involves extremely intricate logical relations.)
The three items analyzed in Table 4 involve the logical operation of "logical addition" as well as the propositional relations of "equality" and "equivalence." These matters have been concisely described by Cohen and Nagel:[18]
Consider . . . the two classes "English books" and "French books." The class which contains either French or English books will be said to be the logical sum of these classes. The operation of combining them in this way will be called logical addition. If a and b are classes, their logical sum is represented by a+b. .. . The symbol + is employed because logical addition has certain formal analogies to the addition of ordinary arithmetic. . . . We may define the equality of two classes in terms of mutual inclusion. Class a is equal to b if a is included in b and b is included in a. . . . In symbols, (a=b)(ais included in b). (b is included in a), where the sign indicates equality between classes, the sign - indicates equivalence between propositions, and the dot (.) indicates the joint assertion of two propositions.
The chief points to be noted about Table 4 are as follows. First, the number of classes involved increases rather regularly as the items increase in difficulty. Second, the relationships between classes become correspondingly more numerous. Third, these relationships may be expressed as propositions holding between classes, hence the passing of each item involves the use of increasingly elaborate propositions about the classes of coins. Fourth, the passing of more difficult items is, for the most part, based upon the simpler logical knowledge involved in passing simpler items. Fifth, a very young child's knowledge of a given concept (for instance "dime") may be thought of as partial: (a) partial in terms of his knowledge of subject matter, and (b) also in the logical sense that certain propositions cannot be made about a class because the child has not yet learned the requisite logical operations which he needs to perform on the class and related classes.
(522)
The use of logical notation in analysis is a reminder that logical operations and relations are intrinsic to the classification of objects. It is obvious that concepts vary in degree of abstractness. This being so, it should be equally obvious that logical manipulations are involved explicitly or implicitly in concept-making, so that these correspondingly vary in complexity as concepts vary.[19]

(523)
Our evidence suggests strongly that young children's logical reasoning is inferior to adults, and that the claims that children reason abstractly should be qualified with statements as to the degree of abstraction involved. [20] Our hypothesis, as well as the more traditional one, explains why children cannot be forced to learn certain subject matters and concepts "ahead of time." Further, when children do not have the concepts which are requisite to certain adult motives, rationales and roles, then these latter should not be attributed to the children. Social psychologists who ignore or understress the importance of concepts, i.e., language, in organizing human behavior are likely to be found anthropomorphizing the child.
SIGN SERIES AND BEHAVORIAL ORGANIZATION
The data, viewed as a progression of increasingly complex logical relations, have implications also for the reductionism implicit in the thinking of many psychologists. Most animal experimentation in this country is based avowedly on the assumption that animal behavior, although less complex, is "essentially" the same as human behavior, and that both behaviors can be accounted for by the same principles. Probably most social scientists do not agree with this view and their disagreement is expressed in the time-honored formula: animals have signals but only man has symbols.
It might be more profitable to view all behavior as organized around signs of varying complexity. This sign series, as it has been called,[21] would account for differences between the activity of lower, higher, and human animals without the necessity for sharply separating one kind of signs from another. The notion of sign series, however, does not in itself answer the question of whether or not each successive level of sign behavior can be reduced to lower levels.
Our Table 4 has some bearing on this controversy. The passing of each more difficult item requires increasingly complex logical manipulation. Although higher order propositions or relations may rest upon lower order ones, they are not thereby reducible. It would require considerable dialectical skill to claim that they are "really the same although more complicated.”
This interpretation is not a negation of the reductionist position-for it cannot be empirically refuted-but represents rather a sharpening of the important problem of the sign series. We view the sign behavior of very young children who have learned to speak as intermediate between that of highest animals and that of adult humans. The research task set by our treatment is that of describing in detail these intermediate steps, and relating them to both simpler and more complex ones.