Some Characteristics of Judgments of Evaluation
Harry L. Hollingworth
AMONG the most common judgments passed in daily life are those which express preferences or aversions, similarities or differences, convictions or doubts, successes or failures, and other " general impressions" or value "estimates." These expressions possess all the characteristics of judgments, but are often said to be "subjective," in the sense that it is impossible or difficult to measure their truthfulness or accuracy by the application of a standardized test. In many cases no "objective" (generally accepted or conventionalized) measure exists, and the only method of test is by observing the internal consistency of an individual's judgments on different occasions, by comparing the individual's judgments with the consensus of opinion of a large experimental group of observers, or by some other statistical criterion. In such cases there is, strictly speaking, no measurement of truth or accuracy, but rather of the consistency, certainty, frequency, or correlation of different judgments.
The dependence of these judgments of general impression on individual differences gives them a particular psychological interest. Esthetic and ethical judgments belong to this group, as do also many verdicts in the fields of philosophy, politics, manners, justice, and most of the decisions of business, pedagogy, and religion. In spite of the practical importance of this type of judgments, experimental psychology has until recently occupied itself with only the more trivial of them. The evaluation of simple esthetic material,—the elements of design, color preferences, tonal harmony, and the various attributes of elementary sensory experiences have been studied in detail. But there have been few attempts to investigate experimentally the characteristics, conditions, and behavior of judgments of such qualities as eminence, interest, belief, persuasion, character, the comic, literary merit, etc.
Studies conducted by the "methods of expression" may be disregarded in this connection, since these methods are expressly directed toward the facts and character of the organic reaction rather than toward the characteristics of the accompanying process of judgment. Of the "methods of impression" various forms have been developed, such as the "method of paired comparisons," the "serial method," "order of merit method," etc. In the hands of different investigators
( 97) these various names have not always meant precisely the same procedure, but the general features of the methods are well recognized. Perhaps the most conspicuous have been the methods of "paired comparisons" and "order of merit." Of these two the latter is by far the more promising and Miss Barrett (1) has recently demonstrated its superiority from the points of view of simplicity, expedition, and reliability and significance of results. The present paper considers some of the characteristics of such judgments of evaluation as those for which the "order of merit" method has been used in the past.[1]
The beginnings of the method may be seen in some of the simple experiments of Fechner, Mantegazza, and Galton. The method was first given definite formulation by Cattell in a study of brightness intensities (2) and particularly in his statistical studies of eminent men and women (3-7). The method has since been used and further developed by many of Cattell's students, including Summer (21). Norsworthy (17), Wells (24, 25), Thorndike (22, 23), Strong (18, 19), Kuper (16), Barrett (1), and the writer (11-14). Downey (8) and Yerkes (26) have also employed the method, and Thorndike (23) has further proposed the transmutation of results secured by this method into a surface of distribution for the purpose of deriving quantitative statements of amounts of difference.
In most of these studies the method has been used chiefly as an instrument in the investigation of some specific problem, such as family resemblance, interests of children, value of advertisements, measurement of school progress, distribution of eminence, etc. But when the various studies are considered as a group there arise a number of interesting problems concerning the judgments themselves. Certain of these problems will here be taken up in turn, with a brief consideration of the data at present available for their solution and interpretation. In many cases the conclusions can be but tentative, and in several cases the problems themselves may ultimately prove to be but "straw problems," suggested by a chance coincidence of accidental or insignificant results. In spite of these facts it seems worth while to present the problems in a more or less definite way, in order that future results may be explicitly referred to them.
Many of these problems were first suggested directly or indirectly in the two very original papers of Wells. The general principle of the method may be given in the words of this author. "Professor Cattell calls attention to the fact that, if one endeavors to arrange
( 98) and rearrange in serial order a number of given objects, the positions successively given them will vary somewhat as they would vary if the arrangements had been made one each by different observers. If we undertook to arrange ten times a series of grays in order of brightness, we should no more get the same order each time than we should get identical orders from ten different subjects. Nor would our own orders vary approximately the same amount from the aver-age; sometimes we should be better, sometimes worse, judges, just as among our ten subjects some would be more discriminative, some less. The judgments of the same individual at different times are theoretically quite comparable to those of different individuals regardless of the factor of times" (25—1).
A fuller description of the method and illustrations of some of its useful practical applications are to be found in the writer's "Principles of Appeal and Response" (14). A further modification, which may be designated the group method as contrasted with the strict order method has been employed by the writer, and possesses several advantages which justify its further development. The following account of this modification is taken from a previous paper (11).
"Instead of arranging the material in strict order of merit the observer placed them in ten piles, according to their `degree of funniness.' In the first pile were placed the superior jokes, in the tenth the poorest ones, while the intermediate piles represented gradation of merit from best to poorest. No instructions were given as to the amount of difference represented by these successive piles, nor as to the number of cards to be placed in each.
Ten observers took part in the experiment, all of whom were women, students in the Barnard laboratory, with one and a half year's work in psychology. When the average position of each card for the ten observers was calculated, the 39 jokes could be arranged in a strict order of merit according to their respective averages. The advantages of this group method are several.
It is much quicker than the strict method, less fatiguing and monotonous to the observer, yet correlates closely with results from the same observers by the strict order method. Further, the method gives opportunity to observe any changes in value of the group as a whole. Thus by multiplying the number of cards in a given group (say 7) by the position of that group (say number 9) and adding these products for all ten groups a figure is obtained which gives some measure of the total value of the series for a given individual or group. Now if the cards are arranged a second, third, fourth, etc.,
( 99) time by the same observers, these sums will indicate the change in total value of the series during the successive trials. This figure is of course not in any sense an absolute measure. It is conditioned by shifts in the individual's standard of value, by his personal variability of judgment, by the variation in standard from individual to individual, and by the fact that no card can be thrown higher than the first nor lower than the lest pile. Nevertheless it affords an interesting and suggestive index of the total series behavior which the strict order method can not yield. It will be shown later that the M.V. (mean variation) in such experiments bears a constant ratio to the number of places into which the objects are to be sorted, so that the relative variability is the same here as in the strict method.
There maybe, in the group method, a certain tendency to arrange stimuli according to qualitative or type resemblance, which might to a degree disturb the judgment of merit,—a tendency, that is, to put all puns in the same pile, etc. But there is no evidence in the results that such an inclination has in any way operated. Moreover the tendency is just as strong, in the strict order method, to put qualitatively similar stimuli in the same region of the scale. Thus Wells found that in arrangements of picture postais according to preference there was a tendency to place near each other cards bearing similar scenes, color schemes, etc. It is conceivable that, even in arranging individuals with respect to scientific eminence, contiguity in space or similarity of field or method may operate as a more or less significant associative factor in determining relative position. But since these factors also help determine the individual's actual judgment of merit, they need not be supposed to warp that judgment in any undesirable way.
In the present experiment each of the ten observers arranged the cards five
successive times, the trials being a week apart. This plan thus gave data for
investigating the variability of the group, of the individual, of the total
value of the series, and of the behavior of each card under the influence of
repetition. Both Wells and Downey have shown that a week is ample time for the
elimination of any great disturbance through the memory factor in the successive
trials."
Problems
First Problem. Variability of Different Parts of the Series. (Repeated arrangements and arrangements by different individuals.) —If all the items are arranged at each trial the variability of each item from its average position may be determined. When this is
( 100) done the variability is usually found to be smaller at the extremes of the series than in the central section, in such material as has been employed. The variabilities increase fairly regularly as the central region of the series is approached. The following records (Table L.) illustrate this tendency. The figures are taken from various studies in which different material and observers were used, and include series of various lengths. The results are not always given for each item, but usually for sections of neighboring items, the sections being determined sometimes by tabular convenience, and in other cases by the way in which the results were originally expressed.
Wells remarks, on this finding in the case of repeated arrangements by the same observer: "We find, as we should anticipate, that the M.V. increases toward the middle position and decreases toward the ends. The amount of this increase varies considerably and constitutes a not uninteresting point of individual difference. In subject A the middle M.V.'s are nearly three times those at the start, in D they are barely half again as much. Individual difference in reliability of judgment seems therefore to be greater in the middle than at the ends. This is what we should expect, for the judgments are more difficult in the middle and we naturally vary more from each other in our judgment of difficult things than in our judgment of easy ones" (25—525).
But the problem can not be so easily disposed of. In the first place the decrease of variability toward the ends is in part a purely methodological consequence, items at extreme top and bottom of the series can be displaced in successive arrangements or by different observers, in only one direction, viz., toward the middle. Even those somewhat further in from the extreme ends can suffer large displacements in one direction only, but at the middle of the series there is double opportunity for large displacement. To be sure the maximum possible displacement is greater in the case of the extremes, since a given card may be displaced the full length of the series, but this situation probably seldom occurs,—would, in fact, occur only in arrangements on the basis of chance. The individual differences pointed out by Wells are then in all probability only differences in variability in general, rather than in specific " amount of increase" from one part of the series to the other.
The problem as it now stands is to determine to what extent the increase of variability toward the center is only a methodological result of this end error, and how far it possesses any further significance. One can not by any means assume a priori that in a given series the middle region will be one of greater difficulty. In fact one
( 101)

( 102) might expect the difficulty to increase regularly toward one end of the series, unless the material were deliberately chosen so as to afford items on both sides of the zero-point of the quality being judged. In the case of the post cards this may well have been the case, and the series may have included positively pleasing and positively displeasing as well as indifferent items. In Wells's study of the series of weights with constant difference ratios between adjacent items, the variabilities increased from the top to the bottom of the series. The same thing was true of Cattell's lists of eminent men, though here there was no lower limit to the series.
Test experiments might be made in which the presence of a zero-region could be introspectively reported upon, with different materials and varying series lengths. Only by such experiments may the rτle of the end error be separated from other suspected influences. The figure of variability has been used as a measure of the amount of difference between the items judged, and whenever this is done it is important to be sure that other conditions are not influencing the size of the coefficients. The table just given indicates that the tendency toward increased variability in the central region is present with varied kinds of material, regardless of the manner in which it is chosen. It will be shown later that the average M.V. of these experiments with judgments of "general impression" tends to be about one fifth of the total number of places in the series. This would mean that the end error might of itself affect the upper and lower quarters of the total series, which perhaps sufficiently explains the tendency to increase toward the center.
Second Problem. Certainty of Individual Likes and Dislikes.—Disregarding the middle of the series the variabilities of the two extreme sections may be compared, since both these sections are equally affected by the end error. Two cases must be distinguished here : (1) The consistency or certainty of repeated arrangements by a single observer; (2) the agreement or disagreement of various individuals of a group. On the first point the following data are available (Table LI.). In this table the first section is to be compared with the last, the second with the penultimate, and the third with the antepenultimate section. It will be observed that the same individual is, on the average, more certain (has smaller M.V.) in the case of the lower sections of the series than in the case of the upper ones. With respect to his data Wells remarks: "Another point of significance is that the M.V.'s are always less at the disliked end than at the preferred end, although there is no intrinsic reason why they should be better grounded in memory. This might be in great part due to a
( 103)
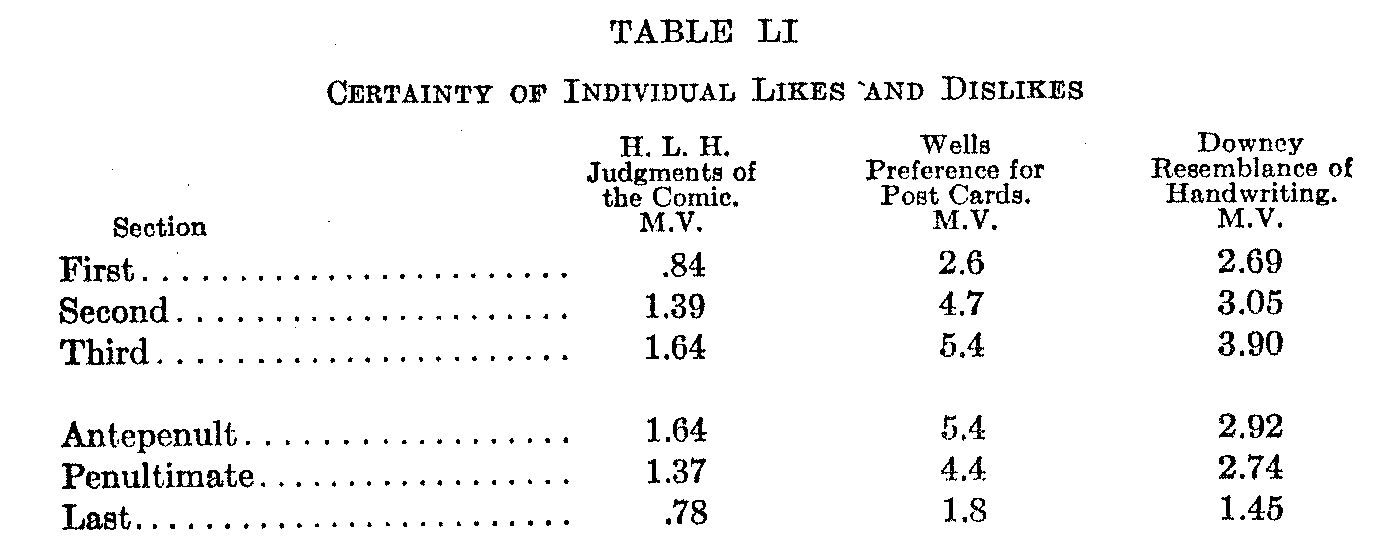
generally unaesthetic series of cards, but it is perhaps generally true that we are surer of our antipathies than of our preferences" (25—525). But Downey finds the same relation shown in general by judgments of resemblance, and remarks: "Toward the close of a series the judgments became judgments of dissimilarity. The records show that such a judgment is frequently made more easily than is a judgment of likeness" (8—20). The writer, in the study of judgments of the comic, finds the same tendency for the lower end of the series to show smaller variability.
Here again then is a problem. In these studies of repeated arrangements the lower end of the series shows the smaller variability. This is hardly to be explained by Wells's suggestion of the greater certainty of our antipathies, unless one can be fairly supposed to entertain feelings of aversion toward "unlikeness" when judging handwriting, and toward lack of humor in an intended comic situation. It should be pointed out that the relation is by no means a unanimous one with individual observers. Only half of Wells's observers show it to any striking degree, though all but one of the five show it when the highest five items are compared with the lowest five. In my own results the relation of the averages is largely due to four of the observers, the other six showing exactly the opposite result. One of Downey's experiments failed to show the tendency with any certainty, and the repeated arrangements of weights in Wells's study showed an increasing variability from top to bottom of the series. It is quite probable that there is no genuine problem here at all and that the results given are merely dependent on the character of the material in the particular cases. It is perhaps easier to find material that is distinctly not beautiful, not comic, or not similar, than to find material of the extreme opposite qualities.
Third Problem. Group Variabilities in Likes and Dislikes.—With respect to the likes and dislikes of the members of a group of
( 104) observers several studies are available. I will present first a discussion of this point as it appeared in the previous paper on "Judgments of the Comic."
"Likes and Dislikes.—If the cards be arranged in a final order of merit for each trial and the M.V.'s of the best cards compared with those of the poorest, that is, if the M.V.'s of the top and bottom of the series be compared, the members of the group are found to agree more closely at the top than at the bottom. Table LII. gives the M.V. for the first and last ten places in each of the five trials. Inspection shows two facts. First, that the M.V. for the top groups, taken either by 5's or 10's, is less than for the lower. Thus the average M.V. for places 110 is 2.03 compared with 2.22 for places 3039. The M.V. of places 15 is 1.97 compared with 2.09 for places 3439.
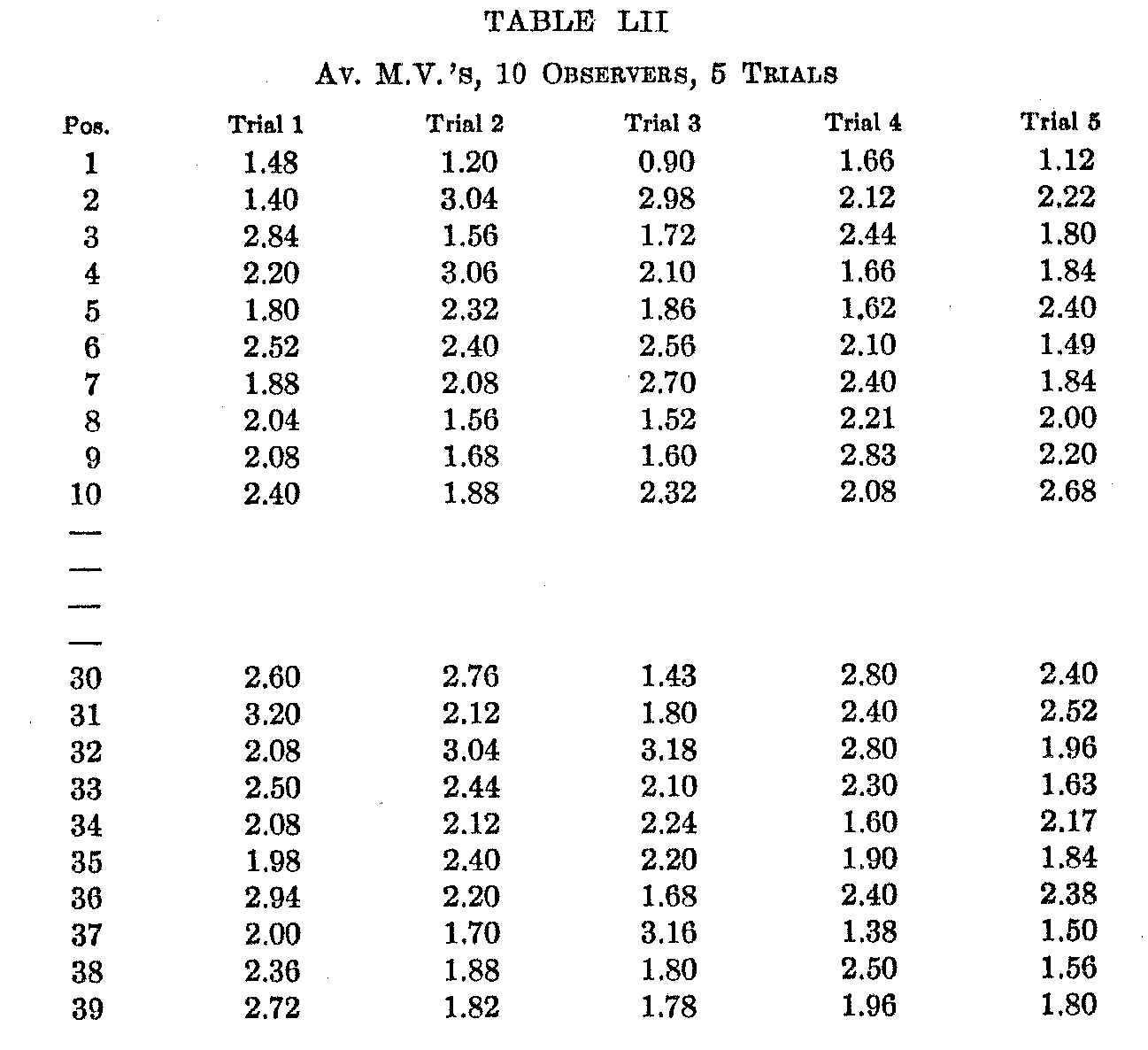
Second, this difference becomes smaller with each repetition, the differences between the M.V.'s of 15 and 3439 being successively .46, .23., .21, .13, .05, and between the M.V.'s of 110 and 3039, being .39, .24, .17, .10, .01. Generalizing we may say that in the beginning individuals agree more closely on the good than on the
( 105) poor, but that with successive repetitions this difference disappears (see Table LIII.).
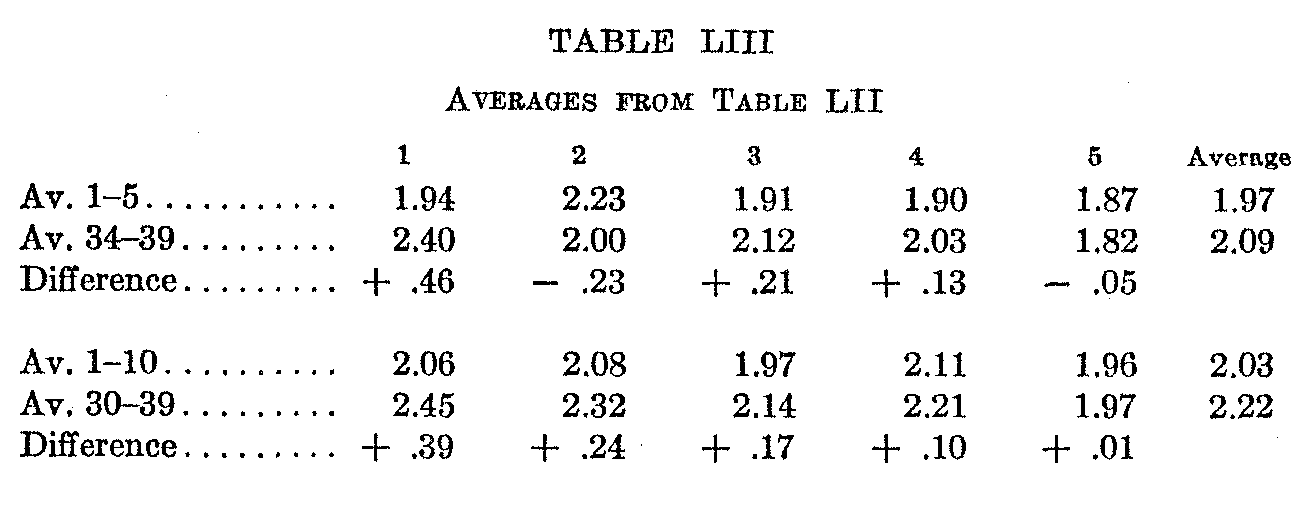
This first relation seems to be a usual one in judgments of this subjective character,—of preference, beauty, persuasiveness, etc. Thus in Wells's study of picture postals, although the author does not call attention to the fact, the figures yield the following result. For places 15 and 4550, the M.V.'s are much alike, being respectively 8.7 and 8.5. For places 110 the M.V. is 8.5 while for 4050 it is 10.2. For 115 it is 9.5 as against 10.3 for places 3550, etc.
Various investigators find that for repeated trials by the same individual the reverse situation holds, the same individual being more consistent at the bottom of the scale than at the top, and the suggestion has been made that this may mean that we are more certain of our dislikes than of our preferences. Giving the present relation a somewhat analogous interpretation, it may mean that although a single individual may be more certain of his antipathies, a group of individuals will resemble each other more in their preferences than in their aversions.
Or the relation may mean simply that we attend to things possessing positive quality, that here where the expression of the judgment is in terms of preference we attend more strongly to the end in which our preferences really lie. But that this is not true for all individuals will be later pointed out. Dearborn finds judgments of unlikeness easier to make than judgments of similarity, and Downey finds some evidence for the same relation, although the average of her results confirms the statement of Wells. But the judgment of preference is qualitatively different from the judgment of resemblance, the one being based on feeling-tone, the other on more restricted perceptual factors.
Another possible interpretation of the data is that the differences between the superior cards, at the top of the scale, are greater than those of the mediocre at the bottom. This was clearly shown by Cattell to be the case in judgments of scientific achievement. Thus
( 106) "The figures show that the average differences [2] between the chemists who are in the first tenth are about eight times as great as between the chemists toward the middle of the list and about twelve times as great as between the chemists toward the bottom of the list." But there are at least three reasons for believing that there is considerable change in attitude when the same observer turns from arranging men according to merit to arranging simple stimuli according to affective tone. The difference lies in the fact that part way down the scale, in the latter case, the expression of judgment changes from terms of decreasing preference into terms of increasing positive dislike, whereas probably few scientists who would get into a total group would be rated as positively bad, the judgment being expressed rather in terms of more or less merit. Arrangements of scientific merit resemble the scale of sensation intensities, varying always in terms of degree, while arrangements of preference resemble the gradation of feelings from the positive pole through a region of indifference to a decided negative pole.
In the second place the suggestion that the smaller variability in the upper ranges depends on objective differences in the stimuli is contradicted by the fact that in the successive arrangements by the same individual four of the ten observers were more consistent in the lower range than in the upper, and this would hardly be expected if the differences between the cards in this lower range were actually smaller than in the upper. Furthermore if something like Weber's law holds for judgments of affective tone as well as for sensation intensity, differences in the upper range would have to be greater in order to yield equal variability, and considerably greater if the variability is still smaller. The whole question of this closer group agreement in the upper ranges seems to merit further investigation and especially, the tendency of the differences to become uniformly smaller in successive trials."
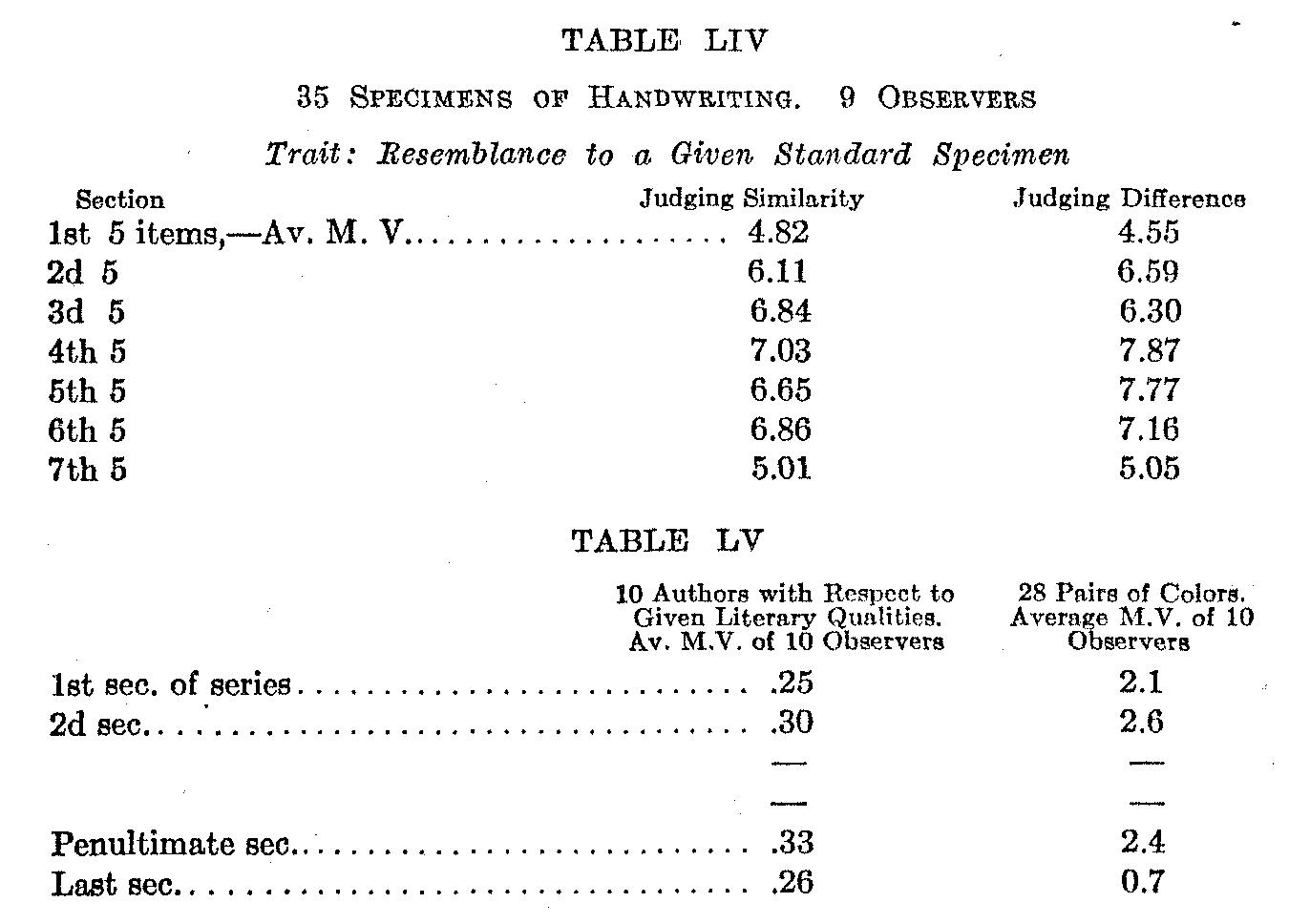
The following results, from the preceding chapter on judgments of similarity and difference in the case of handwriting, show the same tendency. Both when judging similarity and when judging difference the nine observers agree more closely on the upper sections of the series, the material being the same in both cases.
The following table gives the average results of two studies by Wells, the one of "literary qualities," the other of "similarity of two colors." The judgments of literary qualities show the common tendency, but the judgments of color similarities show just the reverse.
( 107)
Individual and class differences in such a tendency might well be expected. In a later study by the writer, in which 50 appeals to specific instincts and interests were rated according to their persuasiveness, an apparently genuine case of such difference is afforded (12). The following table (Table LVI) gives the average
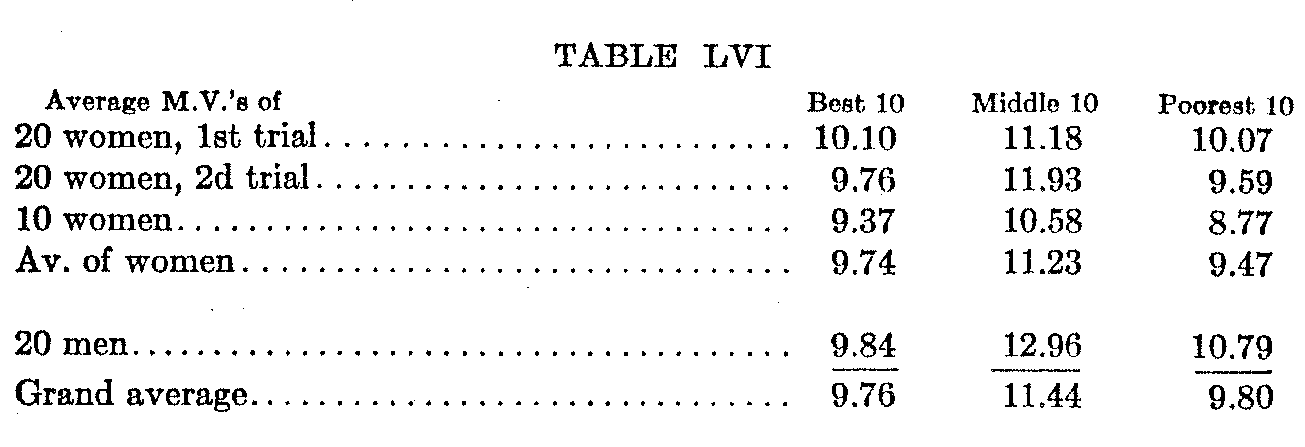
M.V.'s of the highest, lowest, and middle sections of 10 appeals for several groups of observers. The point of interest in these records is the question of closeness of agreement at the top of the list, among the preferences, as compared with that at the bottom of the series, among the dislikes. The evidence here is suggestive. Women seem to agree more closely on their dislikes (M.V.9.4) than on their preferences (M.V. 9.7), but the difference is not large. It is probably reliable and genuine, however, since the relation holds in all three experiments with women. The men, on the other hand,
( 108) agree more closely on their preferences (M.V. 9.8 as against 10.8 for dislikes) and the difference is considerable. The averages of men and women show no difference whatever. There seems to be a sex difference here, which, expressed in general terms, would be, that men resemble each other more closely in their preferences while women are more alike with respect to their aversions. This fact throws some light on the further finding that there is low correlation between the magnitude of the M.V's for the particular cards when the variabilities of the women's judgments are compared with those of the judgments passed by the men.
It is difficult to determine how far this question of group variability at the extremes is merely a function of the material and how far it is due to more essential psychological factors. Such cases as the sex difference just described are obviously not due to the nature of the material, which was the same in both cases. There is further evidence which tends to confirm the suggestion of this sex difference as men and women are now constituted. Thus Strong (18—79) finds that "When women are given an equal opportunity with men to rate appeals (advertisements) they are able to classify their dislikes as well as their preferences, which the men do not. .. . Women have more and greater dislikes than men and are surer of them." Similar evidence is found in Kuper's study of the preferences of boys and girls from 6.5 to 16.5 years of age. "Another sex difference noted was the number of positive dislikes expressed by each sex. The girls gave 161 dislikes as against the boys' 65. Boys seemed to entertain relative indifference toward the appeals at the bottom of the list"(18).
These results, if further verified, would lead to the generalization that men are homogeneous, that is, tend to resemble each other more closely, in the case of their preferences, appeals which are positive and strong; women, on the contrary tending to be alike with respect to their dislikes,—appeals which are weak or negative. Whether this difference bears in the direction of selection and difference in experience or training, or merely toward the temporary motives which operate in reacting toward such experiments, the results do not show. The fact that women have definite and mutual aversions, with fewer common preferences, while men have fewer determinate dislikes but definite and mutual preferences, is, if true, an interesting statistical discovery, and one which may be found to have numerous implications. Whether it be interpreted to mean a fundamental and inherent sex difference or merely a difference which reflects our present social organization (which is doubtless an
( 109) adequate explanation of all the facts) has nothing to do with the present usefulness of the facts themselves. Moreover the suggested further verification must be found before the existence of the difference can be asserted with even mild assurance.
Fourth Problem. Personal Consistency and Judicial Capacity.—This problem was first raised by Wells (25—529) who remarks, in discussing the esthetic judgments of his subjects, "A somewhat significant comparison is afforded between the variability of the (5) subjects from the average of the ten, and their variation from their own judgments (in repeated arrangements). Those who vary least from their own judgments also vary least from the judgments of others. . . . The observations are too few to do more than suggest a general principle, but their interpretation is a rather interesting one. The critic who best knows his own mind would seem the best criterion of the judgments of others." In the case of the judgments of amount of resemblance between colors "the peculiar correspondence between the amount of variation from one's own judgment and from the judgment of others appears" also.
In order to test further the truth of this generalization I have made several experiments in which the variability of the individual (personal consistency, as shown by the correlation of two trials by the same individual on different occasions) is correlated with his degree of agreement with the group average (judicial capacity or representative character). The resulting coefficient of correlation will thus indicate the degree to which high personal consistency implies the representative character of the judgments. The various; coefficients from the different experiments are given in the following table.
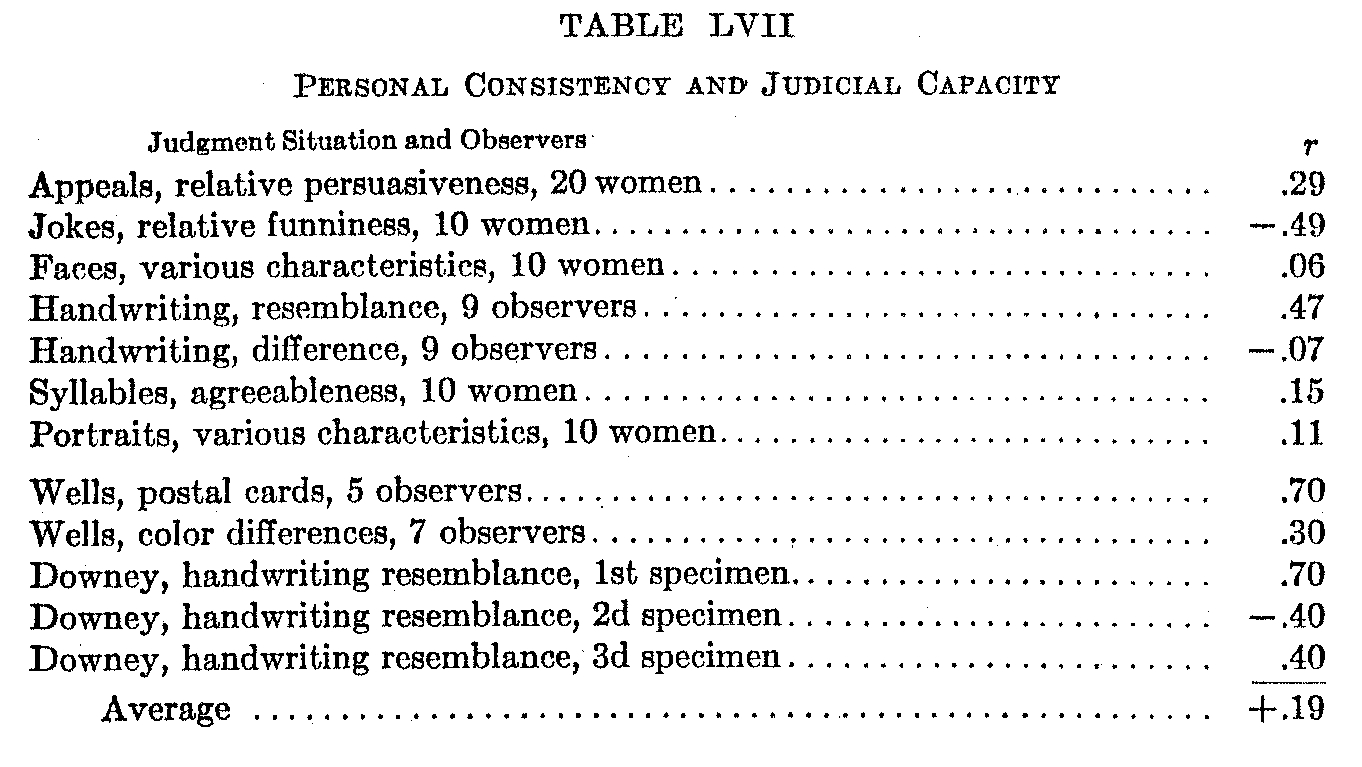
(110)
In my own experiments, with 10 to 20 observers, the correlations are practically zero (Av. .07). I have computed, from the data given by Wells and Downey, similar coefficients from their small groups of observers, (usually 5) and these are also included in the table. Four of the five are positive and large, the other being negative, and the average being .34. The average of the 12 different studies is .19. The only large negative correlation among my own figures is in the case of the judgments of comic situations. It may well be that this single negative coefficient is due to the peculiar nature of the material. The process of adaptation gives to the comic situation a changing rather than a static value. The judgments of the group of observers in this experiment indicate that some of the jokes change greatly in value with successive repetitions. One class, the "objective comic" as I have called them (naive jokes and calamity jokes in which the predicament of the victim is self-induced) rise in the relative scale. Another class fall just as rapidly,—the "subjective comic" (sharp retort, pun, play on words, caricature, occupation joke, etc.). A third class (mixed in character) approximate their original position, in the later arrangements, and constitute about one half of the total series. This gives a waxing, a waning, and a static group.
This means that if a given individual's judgments are to be an index of the opinion of the group his evaluation of the waxing and waning items must vary correspondingly, thus giving him a low personal consistency coefficient. In so far as the individual's consecutive arrangements remain uniform, to just that extent does he fall short of being representative of his group. It is clear from these facts that in all such determinations the stability of the material must be in some way ascertained before the results can be safely interpreted.
Fifth Problem. Personal Consistency in Different Situations. — It would be interesting to know whether an individual who has a high personal consistency coefficient in one situation shows the same characteristic when a totally different sort of material is judged. In Table LVIII. such coefficients are given for 10 observers in two different situations, judgments of the comic and judgments of persuasiveness of appeals. The correlation by relative position between the two columns (1 and 2 of the table) is —.30. The cases are few and the P.E. large, but in 'so far as the data are reliable they indicate no likelihood that an individual who judges the one sort of material consistently will judge with relatively equal consistency in the other situation. The peculiar nature of the material in these two cases gives
( 111) this conclusion merely suggestive value, and further experiments are needed.
Sixth Problem. Judicial Capacity in Different Situations (General Judicial Capacity).—The table just described contains also, for these 10 observers, their degree of correlation with the average of their group in the two experiments (columns 3 and 4 of the table). The correlation between the two columns is .22. This figure again is subject to a large P.E. In so far as it is reliable it indicates a certain degree of general judicial capacity, the individual who is the best representative of his group in the one case being somewhat more likely than any other individual to be the best representative of his group in the other situation.

In another experiment, the results of which are not given in the table, a given group of individuals judged, on the one occasion the legibility of handwriting, and on another occasion their degree of belief in each of a series of propositions. The correlation between representative character in the two cases is just zero (—.01), showing consequently the non-existence of general judicial capacity in this experiment.
Wells found, in his statistical study of literary merit, that the observer who was the best judge (most nearly representative of the group) in the case of "general merit" was not at all necessarily the best judge of the author's possession of the various specific qualities. In a group of 20 observers "the worst judge of general literary merit, according to his divergences, is the third best judge of charm, the best judge of clearness, and the thirteenth best of euphony. The best judge of general merit is the fifth best of charm, the fourteenth of
( 112) clearness, and the seventeenth of euphony. . .. We can hardly draw inferences as to the general capacity for sound judgment as measured by the soundness of judgment for any particular class of objects ... the fact that one has a good judgment for psychologists tells us very little about the value of his opinion in other fields. . . . To demonstrate the very existence of an abstract power of judgment is ultimately synonymous with the problem of free will" (24—30).
Cattell found, in the case of the judgments, by ten psychologists, of the eminence of fifty living psychologists, that "the second best judge of the first ten psychologists is the worst of the second, the fifth of the third, the eighth of the fourth, and the sixth of the fifth" (24—30). On the whole then, there is no evidence, in the available material, of the existence of such a thing as general judicial capacity.
Seventh Problem. Relation of Variability to Series Length. — Another striking relation brought out by the comparison of various order of merit arrangements of stimuli on the basis of such affective factors as preference, beauty, persuasiveness, funniness, etc., is the constancy of the ratio of the average M.V, for the series as a whole to the number of possible positions in the range. If by M.V. we designate this average variability and by P the total number of positions in the scale then M.V./P is, with various kinds of material, with different groups of observers, and with a widely ranging value for P, usually .20, and with high reliability. The following table exhibits this relation in such material as the writer has at hand.
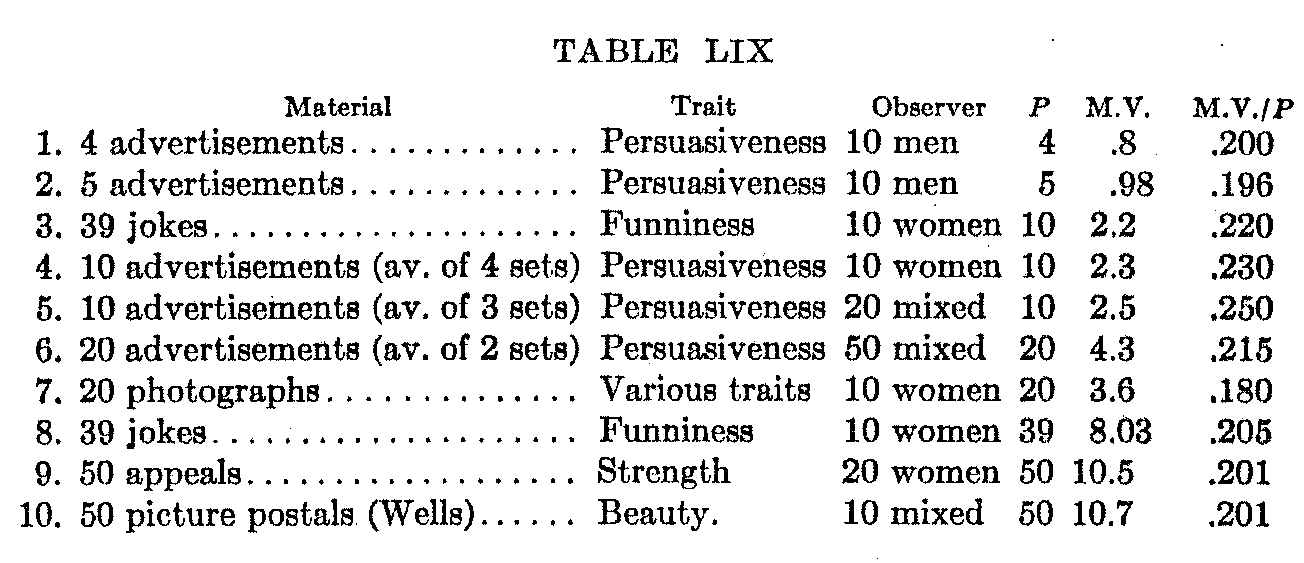
That is to say, the M.V. is always about one fifth of the total number of possible places, or the P.E. (probable error) assuming a normal distribution, about .168 or about one sixth of the range. The evidence seems to the writer too strong to permit of explanation in terms of mere coincidence. Of course if the material had been the same throughout, the only variable being the number of places into
( 113) which it was sorted, this is just what we might expect, for the relative P.E. would remain constant, the absolute P.E. depending on the fineness of the grades of distinction. But we have here ten distinct sets of material, judged in terms of a considerable range of traits, by widely differing groups of observers, both as to sex, training, interest, and number. The only constant factor is that the judgment is always based on the affective reaction to the stimulus. And we find that in every case the probable error is approximately one sixth of the range. (It would probably be slightly larger if it were not for the fact that the end error tends to reduce the variability of the extreme upper and lower positions.) Assuming that the M.V.'s were equal in all parts of the range (and they do not vary greatly), and allowing a P.E. in both directions from both the upper and lower
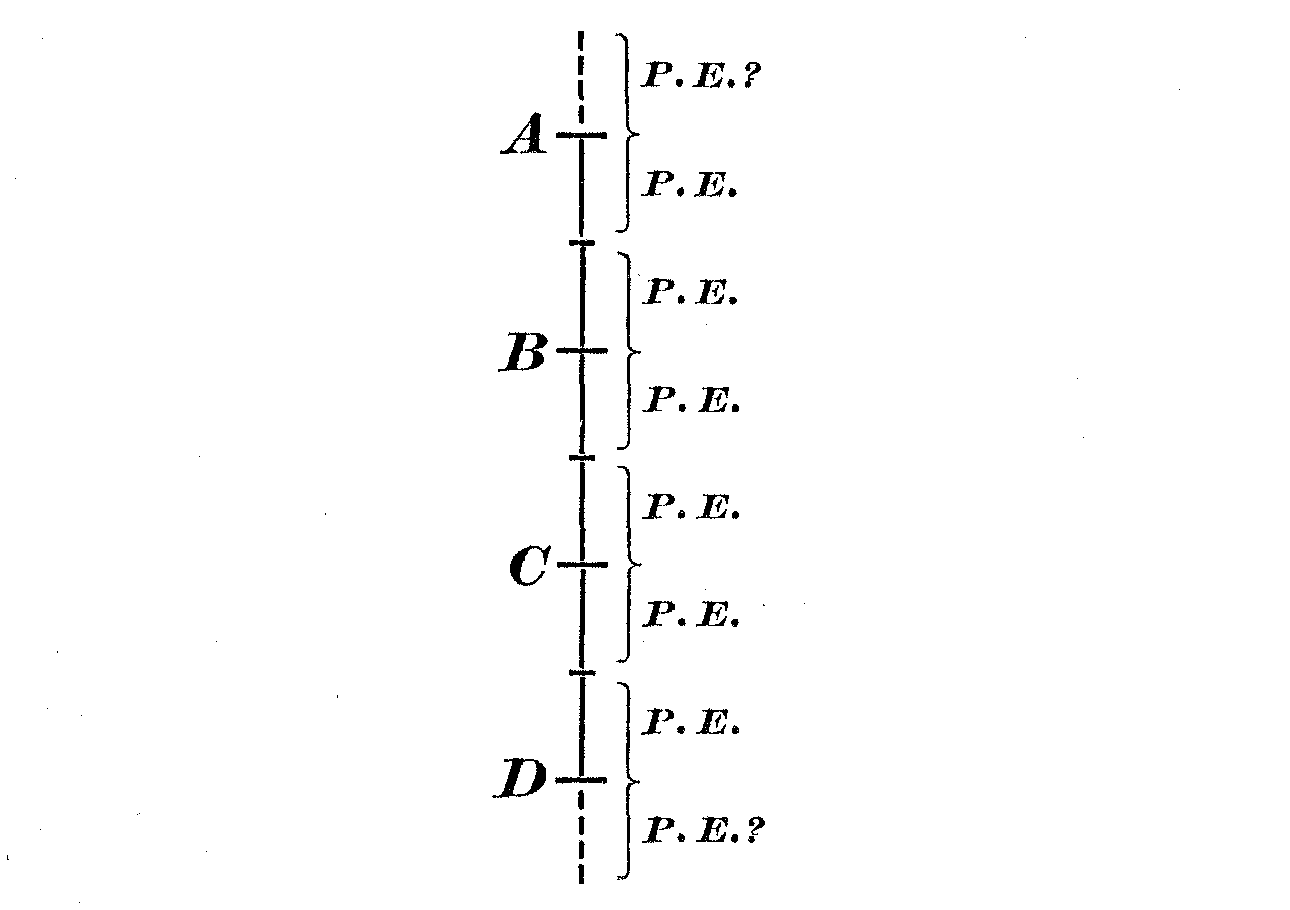
extremes, the total range would then be divided into four sections, each separated from its neighbor by the respective P. E.'s, somewhat as follows. This would mean that, so far as the average judgment of the group of observers is concerned, there are only four distinct grades of difference or merit in the material, only four shades of distinction on which the group would, in the long run, agree, these grades corresponding to the sections lying about A, B, C, and D as central tendencies.
This situation is curiously analogous to that disclosed in judgments of the same observer, where practise shows that about four or
( 114) five distinctions of certainty, clearness, etc., are all that can be comfortably and accurately made. The same thing that holds for the variability of the individual holds for the variability of the group. And the fact that the law holds for such different kinds of material and traits argues an interesting resemblance between the judgments involved in such affective discriminations.
The size of this ratio M.V./P would become smaller as the material came to be selected so as to disclose more pronounced or more objectively measurable differences. Thus in judgments of resemblance of penmanship, which are supposedly more directly perceptual and objectively verifiable in kind, Downey finds M.V.'s which, if arranged as below, according to the range of possible positions, would yield an M.V./P value of about .163, or a probable error of about .130, meaning that while there are only about four clearly marked grades of beauty, funniness, persuasiveness, etc., there are about five clearly marked degrees of resemblance.
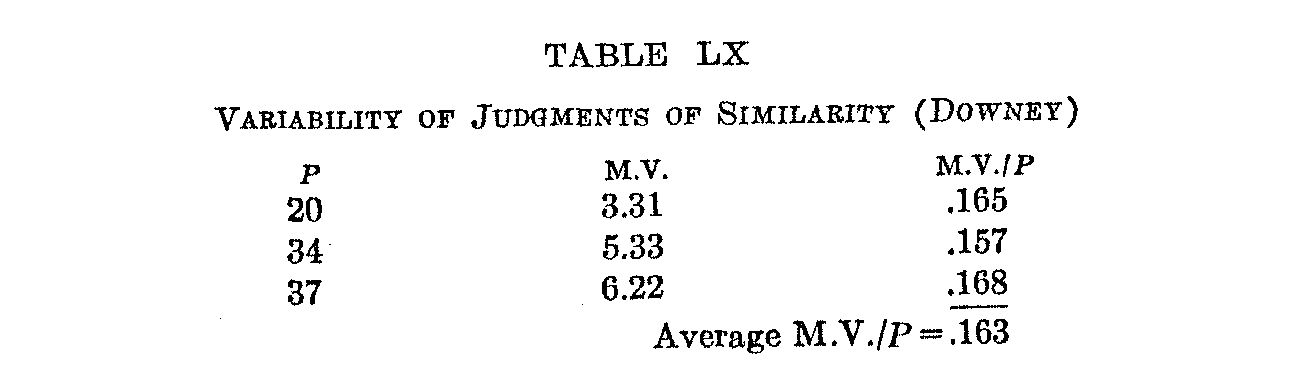
It is probable that this ratio (M.V./P) can be used as a reliable index of the objective character of judgments and with greater accuracy than the crude M.V. employed by Wells. Using this ratio the objectivity of his three classes of judgments would be, in increasing order,—preference .201, weights .141, colors .086, showing that the judgments of weight order were more subjective than those of color order, thus reversing the order assigned.
Eighth Problem. Quantitative Criteria of the Subjective.—The next problem grows directly out of the preceding one, and has to do with the proposed "quantitative criterion of the subjective." Wells writes: "So far as any distinction on a statistical basis is possible we might consider as subjective those types in which the various judgments of the individual formed a species of their own, varying from each other considerably less than from an equal number of judgments made by different individuals; and consider as objective those in which an individual would vary from his own independent judgments about as much as the variation of an equal number of
( 115) judgments by different individuals. . . . The two categories would almost certainly be continuous" (25-512).
A determination of these criteria for materials affording three classes of judgments was the primary purpose of Wells's study. His conclusion may be given in his own words : "It has appeared that in the first class (the highly subjective feeling of preference for different sorts of pictures) the judgments of each individual cluster about a mean which is true for that individual only, and which varies from that of any other individual more than twice as much as its own judgments vary from it; that in the second class, with the colors, the variability of the successive judgments and that of those by different individuals markedly approached each other but still preserved a significant difference; while in the third class;, with the weights, we found that there might be even an excess of the individual variability over the `social.' This comparison seems to afford, to a certain extent, a quantitative criterion of the subjective" (25-547).
Further determinations of a somewhat similar sort may be derived from many of my own studies. Instead of using a figure of variability I have employed the coefficients of correlation. The significance should be the same and fewer trials are required to determine the results.
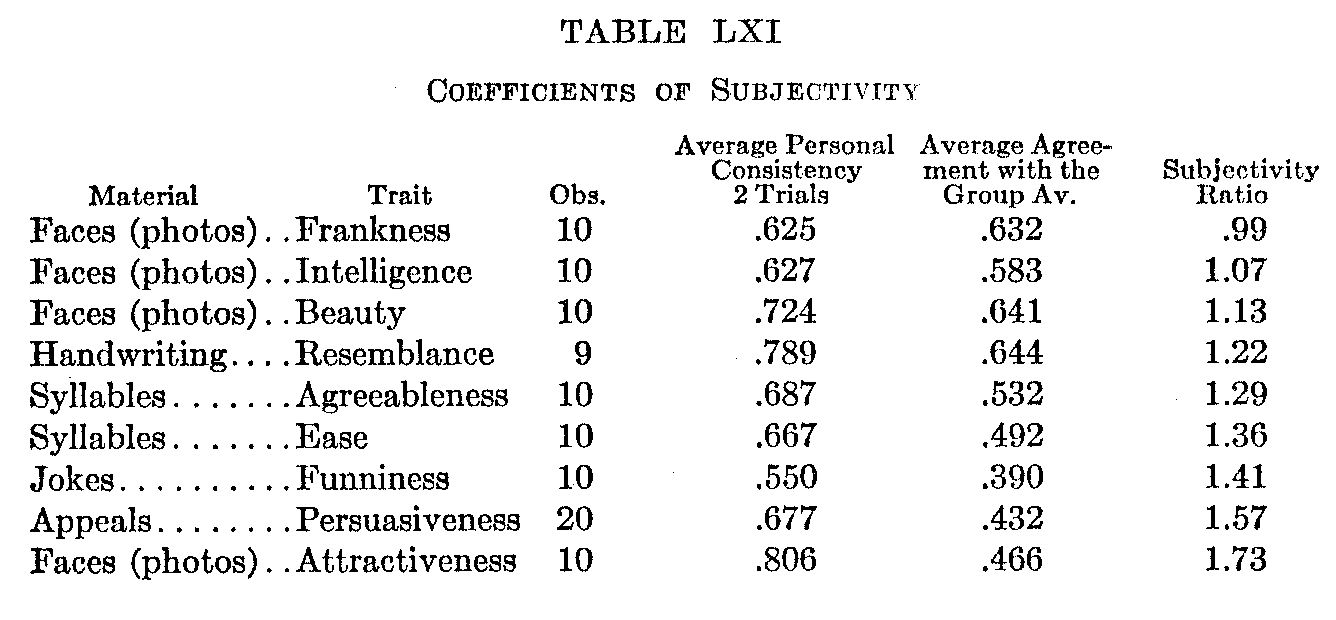
Table LXI. gives a series of these determinations. The various materials and traits are arranged in an order of increasing subjectivity as measured by the "subjectivity ratio" (ratio of index of personal consistency to index of group agreement). Judgments of the frankness and intelligence of faces (photographs) are completely objective, that is, a given individual correlates as closely with the average judgment of the group as he does with his own judgment on another occasion. But as one goes on down through the table the
( 116) personal consistency coefficients remain fairly constant while the coefficients of group agreement decrease. This gives a larger and larger "subjectivity ratio," until, in judgments of the attractiveness of faces, the personal consistency coefficients are nearly twice as large as those of group agreement.
The use of the coefficients of correlation as criteria of subjectivity in the case of judgments expressed by serial arrangement is much more satisfactory than the relation of the two figures of variability. Fewer trials are required for the determination, and the measures are not complicated by the end error, and other factors which tend to disguise the real size of the M.V.'s.
It is probable, however, that the distinction between subjective and objective judgments is at best but an artificial one. The chief difference between the two classes seems to consist in the amount or clearness of the differences present between the various items of the material judged. Judgments of preference will, in the case of a given individual, be expressed as consistently as judgments of weight, duration or intensity, providing the differences are equally perceptible ; and judgments of intensity, etc., will vary as much as those of preference if the differences afforded by the material are sufficiently slight. The fact that a so-called objective scale may be applied to the material in the one case and not in the other, is, in the first place, only an extrinsic fact, and in no way conditions the psychological act of judgment. In the second place the objective scale derives its own validity in the long run only from the consensus of opinion and from its pragmatic value. So far as this is concerned a consensus of opinion may be secured for even the most variable and personal sort of material, as witness Thorndike's scales for measuring the excellence of penmanship, literary composition, drawing, etc. The only difference between the two cases would be in the universality of the verdict, and this again in no way conditions the psychological act. It is apparent that the coefficients are merely indices of certain characteristics of the material, rather than of any features of the judgments, as judgments. A certain sort of material may not be constant from time to time or from observer to observer (jokes or comic pictures, for examples). Here the judgment attitude may be conceived as constant, but the material changed. Or one sort of material may provide larger differences between items most alike, and either situation would be revealed by the "coefficients of subjectivity. "[3] It
( 117) is to be expected that various sets of material, of the same content but with differing degrees of difference between successive items would show the same differences in "subjectivity" as those found with different kinds of material. Subjectivity means, then, either of two things, or both: (1) The amount of difference, (2) the universality of the verdict. These also differentiate judgment and perception.
Ninth Problem. Agreement Between Diverse Groups.—The final problem to be presented here concerns the agreement between the average judgments of two groups of observers, when only small groups are used. It is of course obvious that if the two groups are sufficiently large and represent similar or random selections of humanity, the two final orders will be identical, no matter how "subjective" the material may be. But if the groups are small, or if they represent different samplings of human nature, differences might be expected which would be of interest to individual, social, and applied psychology.
I have brought together in the following table such material as I have been able to secure from my own studies and from the published reports of others. The range of material represented is small, and this problem would seem to constitute an interesting theme for further work in statistical psychology.
In the case of this sort of material the average correlation of two groups representing approximately the same sampling of the popula-

(118) -tion is about .60. The average personal consistency coefficient is about .70, while the correlation of two trials by the same group on two different occasions is about .90. The coefficient of personal consistency thus stands about midway between that of the consistency of a group and the agreement of two diverse groups.
The last two figures from Strong's data, and the one from Kuper's study show the great degree to which the group agreements are conditioned by the composition of the groups. The college students and the manual laborers yield a large negative coefficient, while the two groups of college students give almost perfect positive correlation. The boys and girls correlate, in judging the interest of pictures, by only .24. When college students or adult men and women judge the degree of their interest in appeals not remotely different in character from those used with the children, men and women show as high correlation as do two groups from the same sex. It would seem that in this index of group correlation we have then another useful index of the subjectivity of the material. If the material were weights or brightness intensities there would be no reason for expecting these various groups to show any significant differences in the degree of mutual correlation.
We are thus provided with at least five different indices of subjectivity,—personal consistency, approximation to group average, the ratio of these two indices, the ratio of variability to series length (M.V./P), and the agreement of diverse groups. It would be interesting to work out the interrelations of these various indices in different judgment situations.
BIBLIOGRAPHY OF THE ORDER OF MERIT METHOD
1. Barrett, The Order of Merit Method and the Method of Paired Comparisons, Jour. Phil., July 3, 1913, 382-4.
2. Cattell, The Time of Perception as a Measure of Difference in Intensity. Phil. Stud., 1903.
3. Cattell, A Statistical Study of Eminent Men, Pop. Sci. Mo., 53, 357, 1903.
4. Cattell, Statistics of American Psychologists, Am. J. Psychol., 1903, XIV, 310.
5. Cattell, Statistical Study of American Men of Science, Science, N. S., XXIV.
6. Cattell, A Further Statistical Study of American Men of Science, Science, N. S., XXXII.
7. Cattell, Appendix, American Men of Science, 2d ed., 1910.
8. Downey, Study of Family Resemblance in Handwriting, Bulletin No. 1, Dept. of Psychology, Univ. of Wyoming, 1910.
9. Fernald, G. E., The Defective Delinquent Class, Differentiating Tests, Amer. Jour. of Insanity, 69, 125-142, 1912.
10. Hillegas, Milo B., A Scale for the Measurement of Ability in English Compositions, Teachers College Studies.
( 119)
11. Hollingworth, Judgments of the Comic, Psych. Rev., 1911, 18, 132.
12. Hollingworth, Judgments of Persuasiveness, Psych. Rev., 1911, 18, 234.
13. Hollingworth, Influence of Form and Category, Jour. Phil., 1912, 9, 513.
14. Hollingworth, Principles of Appeal and Response, Appletons, 1913.
15. Hollingworth, Experimental Studies in Judgment, ARCH. Of PSYCH., No. 29.
16. Kuper, Group Differences in the Interests of Children, Jour. Phil., 1912, 9, 376.
17. Norsworthy, Validity of Judgments of Character, Essays in Honor of William James, 1908.
18. Strong, The Relative Merits of Advertisements, ARCH. of PSYCH., 1911, 17.
19. Strong, Application of the Order of Merit Method to Advertising, Jour. Phil., October 26, 1911, 600-606.
20. Strong, Psychological Methods as Applied in Advertising, Jour. Ed. Psychol., Sept., 1913, 393.
21. Sumner, A Statistical Study of Belief, Psych. Rev., 5, 616.
22. Thorndike, Handwriting, Teachers College Record.
23. Thorndike, Mental and Social Measurements, 2d ed., 1913.
24. Wells, A Statistical Study of Literary Merit, ARCH. of PSYCH., 1907, 7.
25. Wells, On the Variability of Individual Judgments, Essays in Honor of William James, 1908, 511.
26. Yerkes, Introduction to Psychology, Holt, 1911, Ch. XIV.