The Structuring of Events: Outline of a General Theory with Applications to Psychology
Floyd Henry Allport
Maxwell Graduate School, Syracuse University
I. THE PROBLEM OF STRUCTURE
It is generally assumed that the way to understand nature lies in the understanding of its laws. Some predictability and order in the objects studied are a prerequisite to knowledge about them. It is frequently assumed, also, that the laws of nature are essentially quantitative—that they express amounts of some measurable attribute and relationships by which one such variable is a function of another. Hull and his associates stated the matter as follows: "Since it appears probable that everything which exists at all in nature exists in some amount, it would seem that the ultimate form of all scientific postulates should be quantitative" (2, p. 8).
The purpose of the present article is to explore the possibility that, notwithstanding the ubiquity, precision, and unquestioned importance of quantitative and covariational formulas, there may be in nature another type of law that is quite as universal, objectively demonstrable, and, in its way, precise. The writer believes that this is true and that the knowledge of such a possible nonquantitative, but still fundamental, law (which, however, is neither "qualitative" nor "configurational") is as indispensable as quantitative formulations for a full understanding of any phenomenon, and that it is particularly needed at the present time in the field of psychology. It is to knowledge of this sort that we must turn for further illumination upon that still unsolved but vital problem, the organization of behavior. However useful they may be for descriptive purposes, the molar laws of covarying behavioral quantities have about reached the end of their tether so far as explanation is concerned. Some broader theoretical outlook is required if the treatment of these variables themselves is to acquire a deeper and more useful meaning. It is to the meeting of this theoretical need that the present article is addressed.
A word of admonition, however, should be said about its content. It must deal with issues that transcend psychology and pertain to all the sciences; for the problem of the nonquantitatively lawful in nature is universal. At first it might seem that the theory to be proposed, since it must be stated in correspondingly general terms, lies outside the scope of psychology proper. This impression would be erroneous. Though the reader may miss some of the familiar terminology, and though for want of space it will be necessary to ask him to make some of the applications for
(282) himself, the projected general model pertains at every turn to the task of explaining the fundamental processes of behavior. Among the problems upon which it specifically bears, within the limits of the present article, are the nature of psychological organization, motivation, learning, perception, and their interrelationship, the continuity-versus-discontinuity controversy, facilitation and inhibition, and the energies of attitudes. The writer believes that the theory is the more significant for psychology precisely because it has been developed in a wider frame of reference to meet a more universal challenge in science.
Let us begin by re-examining the role of quantitative statements in generalizations concerning behavior. The reader will find below a description of a familiar act or act sequence. The description is given wholly in terms of quantitative laws. Some of them are repeated as called for in the act, and nearly all are of the covariation type. The list is divided into five phases (A to E) to correspond to successive phases of the act sequence. Let us see how well the list describes and explains the phenomenon and whether we can identify the behavior involved.
A
1. The rate of evaporation varies with the temperature.
B
2. The curvature of the lens varies inversely with distance from the object of vision.
3. A neural impulse occurs at full intensity or not at all.
4. The magnitude of a neural impulse varies directly with the diameter of the neuron.
5. The intensity of a sensation increases directly with constant relative increments of the stimulus.
6. The more continuous the contour of an object the more readily it is perceived.
C
(3.) A neural-transmission impulse occurs at full intensity or not at all.
(4.) The magnitude of a neural impulse varies directly with the diameter of the neuron.
7. The energy of a muscle contraction varies directly with the number of muscle fibers excited.
Laws, 3, 4, and 7 now reappear in several repetitions, and, in connection with them, laws such as 2, 5, and 6.
D
8. The terminal velocity of a falling body is equal to the constant acceleration of gravity times the duration of the fall.
E
(3.) A neural-transmission impulse occurs at full intensity or not at all.
(4.) The magnitude of a neural impulse varies directly with the diameter of the neuron.
(7.) The energy of a muscle contraction varies directly with the number of fibers excited.
There are repetitions of this series, interspersed with earlier laws.
(8.) The terminal velocity of falling is equal to the constant acceleration of gravity times the duration of the fall.
9. The velocity of flowing varies inversely as the cross section of the flow.
If the reader now tries to state the behavior represented by the above list, he will probably be somewhat bewildered. He will guess that the phenomenon involves principles of gravitation and hydrodynamics along with behavior; but he cannot go much further than this with certainty. One wonders whether quantitative laws can be expected to explain an act sequence that they do not describe with sufficient completeness to permit its identification. Furthermore, there are important questions about the laws themselves that are unanswerable from the list: (a) Why are these particular laws brought together here, rather than countless others that could be mentioned? (b) How is their order in the list to be accounted for, including the repetitions indicated? (c) There appears to be very little "organization" of the laws in the list. Some organizing principle is
(283) needed to help us understand what is happening. We look in vain for answers to these questions in the laws themselves. There is something essential that they fail to give.
Let us now redescribe the act sequence in other, more familiar, terms, using the same interspersed capital letters to indicate the various stages:
(A) A small boy on a warm day, becoming thirsty,
(B) sees a pitcher of lemonade and a glass on a buffet.
(C) He goes to the dining room table, pulls out a chair, places it near the buffet, climbs upon it, pours lemonade
(D) from the pitcher into the glass,
(E) raises the glass . . and drinks.
Now the matter is clear. By the use in this description of some terms other than quantitative we have been able to state the act sequence intelligibly. We are also able to answer, even on the basis of the meager knowledge of the events thus provided, all three of the questions about the quantitative laws themselves that these laws failed to answer. If we read the laws again, this time in conjunction with the acts listed above for the appropriate parts of the sequence, we can see the true basis of (a) the selection, (b) the ordering, and (c) the organization of the laws as they are "called into play." Something other than quantities of happenings has now been added to the picture, with a resulting increase of our understanding. The significance of the laws is clarified by showing that they are "contained," as it were, and ordered within a given self-delimited arrangement of happenings. Let us call this new "something" that is added to the quantitative laws in the form of a pattern of happenings the structure of the phenomenon in question. It will be seen that by this term we are not referring to anything that is "static." It is, rather, a dynamic structure—a structure of events.
Structure then, as thus defined, is what the quantitative laws fail to give; and it is what is needed (and needs more fully to be explained) if we are to have an adequate understanding of behavior. The structuring of events, to be sure, never occurs without the fact that the laws also hold good. Quantitative laws are demonstrable in all phenomena and are highly important and useful. Nevertheless our analysis shows that structure also is something that "holds good" and that must be considered in its own right. It seems possible that it may have laws of its own. If so, these laws will probably be of a different sort from the other (quantitative) laws; for we have seen that the latter do not describe the structure of phenomena and that the gaining of an inkling of the structure was necessary in order to answer certain questions about the quantitative laws themselves. We can go even further and say that if it were not for such a structure (comprising events of stimulus impingement, neural excitation, muscle-fiber activation, and the like), there would be no way of showing that the quantitative laws of behavior exist. The understanding of dynamic structure is therefore a matter of considerable importance.
Our statement of the laws in the example given was admittedly crude. Neither the definite equations nor specific quantities were given. If they had been stated more precisely and exemplified by quantities, would they then have been able to supply the necessary information and to identify the act sequence? It seems doubtful, since the added elements would still be abstractions so far as the actual pattern of events is concerned. It is true, also, that only a "sample" of the possible covariation laws was given. Suppose the list had been extended until it covered all the equations that could apply to a
(284) boy's getting a drink of lemonade (no doubt a very great number). Could the problem of the pattern have been solved then? This, too, is doubtful. If the laws were rigorously limited to quantitative statements, the task might have been even more difficult than before. We shall probably have to conclude, then, that the failure of the quantitative laws to be fully descriptive and explanatory does not lie in the paucity of the laws available nor in a lack of precision in their statement. It lies, rather, in their inherent limitation with respect to the problem in hand.
It is true that the glimpse of structure that illuminated the second approach to our example had to be inferred from a molar account, which, like molar statements in general, provided very little of the actual detail of structurization. Still, it served to recall, from other experiences, what we did know about the structure of the organism's behavior, including its neurophysiological aspects in their relevance to the episode in question. The most pressing present problem for psychology, in the writer's opinion, is to pass from such crude molar descriptions to a closer analysis and delineation of the structure of behavioral acts. What is latent or implicit behind molar formulations that can give the illumination which quantitative laws fail to provide? We should not beg the question by saying that unless structure can be stated in quantitative terms it is unlawful and cannot be explained. The quantitative laws themselves, even "molar" laws, require some structural understanding. Nor can it be said that structure lacks generality. What could be more universal in behavior than the "general format" of eating or drinking, or of a hundred other behaviors sufficiently stable and recurrent to have been given a name? But the problem is broader, even, than the field of psychology.
Evidences of structures of a generalized sort occur in the phenomena of every science. If such structurings are general, and if they cannot be explained by quantitative laws, is it not logical to suppose that there may be such things as structural laws, that structure is something sui generis? There might even be some one universal structural principle that operates throughout the whole of nature.
The history of psychological schools and theories could, in a sense, be regarded as the record of attempts to deal with this problem in the field of psychology. They range from totalistic concepts such as gestalten, sign gestalten, supersummative wholes, cognitive maps, topological and brain fields, and "hypotheses," through open systems, mechanics of redintegration, communication and information, and mathematical brain models, to the stripped intervening constructs of behavior theory. Metaphysical postulates, also, such as "emergence," "entelechy," and various "manikin" assumptions have not been wanting. No final and conclusive answer has yet appeared. The very diversity of these efforts attests the difficulty of finding some clear, denotational way in which the structure of behavior can be described.
Perhaps the most general reason for the failure to solve the problem lies in the fact that it has not been approached in its own right. It has been assumed, in effect, that there is no general structural problem, that the means are already at hand for explaining each specific structure by the traditional methods of scientific logic. On the one hand it is assumed that, since every event must have some cause, the ordinary logic of causality should be able to explain the "structuring" of events. That we have not been able to explain matters this way is due merely to the fact
(285) that we have not yet found the right cause. On the other hand, there is a tendency to believe that the laws which state covariations and thresholds of measurable quantities should be able to bring it about that each element of a phenomenon gets placed in the proper spatial position at the exact time and sequence required for its characteristic structuring. The fact that no one has been able to show how quantitative laws accomplish this feat has not been sufficiently taken to heart. It is forgotten that quantitative laws are merely descriptive statements, not causal agents or forces. Frequently a "mechanism" of some sort (a term borrowed without justification from mechanics) is "postulated," through which the laws are believed to "act," or within which they are said to be "manifested," and into which "intervening variables" can be injected to fill the gaps in our structural apprehension. The writer has discussed the assumptions underlying the belief that quantitative, or mechanical, laws are the "architects of structure" in a forthcoming work (1). We shall here turn our attention to the problem of "structural causality."
II. CAN STRUCTURE BE EXPLAINED BY "CAUSE AND EFFECT"?
According to the commonly accepted definition of cause and effect an event,
0, is the "cause" of an event, P, if it precedes P and is a necessary and
sufficient condition of P. If O then P; if not O then not P. If we employ the
symbol
![]() to indicate contingency and a superimposed dot to show negation, this
can be expressed as
to indicate contingency and a superimposed dot to show negation, this
can be expressed as
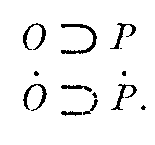
Causes and effects can also be written as a linear series of single elements in which each succeeding effect becomes a cause for the next effect, thus:
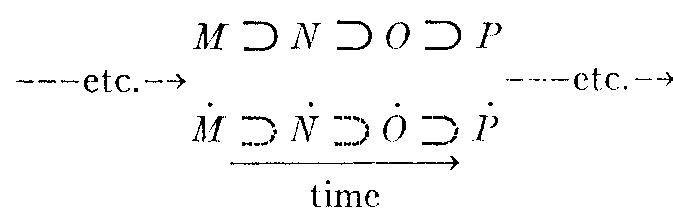
Time is here represented as a linear stream, and no limit can be placed upon the number of cause-effect pairs that precede the series shown or that follow it. In psychological theories such limited series as shown above are illustrated by linear sequences such as stimulus—receptor excitation—afferent neural excitation—central neural excitation —efferent neural excitation—muscle fiber contraction. Something like this is implied in the Hullian system in the "linkage" between the stimulus process and the reaction. There is, however, no logical reason why the causal series should not be extended indefinitely at both ends. We shall presently consider this possibility in the example of the boy who is getting a drink of lemonade. This historical method of causality explanation is seldom carried through in explaining the phenomena of behavior, or indeed anywhere else. A certain part of the chain is delimited as "belonging" to a particular behavioral act or other phenomenon; and the remainder of the sequence is ignored. The fact that this can be done without being aware of any arbitrariness is itself an evidence that some principle other than linear causation must be at work. To find this principle is our present task.
But it is probable that events do not happen in the single-chain fashion just indicated. O may be a necessary condition of P, but it is usually not a sufficient condition. Other events, O', O", O"', and so on, must be present together with O in order to predict the occurrence of P, even though the absence of
(286) any one of them might negate P. And similarly, each of these O's may have behind it another compound set of earlier "causes." This situation, which is still linear in its sequences, is familiarly known as "multiple causation." It is represented in behavioral theories by such concepts as stimulus compounds, drive stimulus added to object stimulus, and attendant reinforcing conditions. Such a compounding of causes makes the definition of causation as a necessary and sufficient condition somewhat inapplicable right at the start.
But to proceed further, let us note that a number of manipulanda in the environment are frequently required for the description of a behavioral act. The chair, pitcher, and glass were prerequisites in the boy-lemonade example. Let us call the events of contact with such objects P, Q, R, etc. Now behind each of these objects there lies a cause-effect sequence that extends indefinitely into the past and ramifies in space. Let us take the boy's contact with the chair as P. An earlier 0 existed in the form of someone's placing the chair at the table. Behind this, at a still earlier time, was the matter of purchasing the chair, a happening which might have had multiple causation (O's) in acts of conferring between the boy's father and mother and in the combined acts of sales clerk and cashier. Behind these was the act of the store's manager in having previously "stocked"the chair, and behind this were many happenings involved in transportation, each of which, in turn, had its multiple precursors. For example, prior to the "loading of a chair"there were acts of a number of workmen in a factory handling tools and materials in the making of the chair. And again, prior to both the materials and the tools lay multiple occurrences such as wood cutting, fabrication, transportation, and so on. As the linear series is traced backward in time it is seen to spread out in space as a "regressus pyramid." By the time we have traced it backward only a few steps the number of 0's (and P's) required to account for the contact of the boy's hand with the chair is so great that prediction from any one event has only a negligible value. Merely to illustrate the well-known regressus expansion (rather than for any intrinsic value it may have) Fig. 1
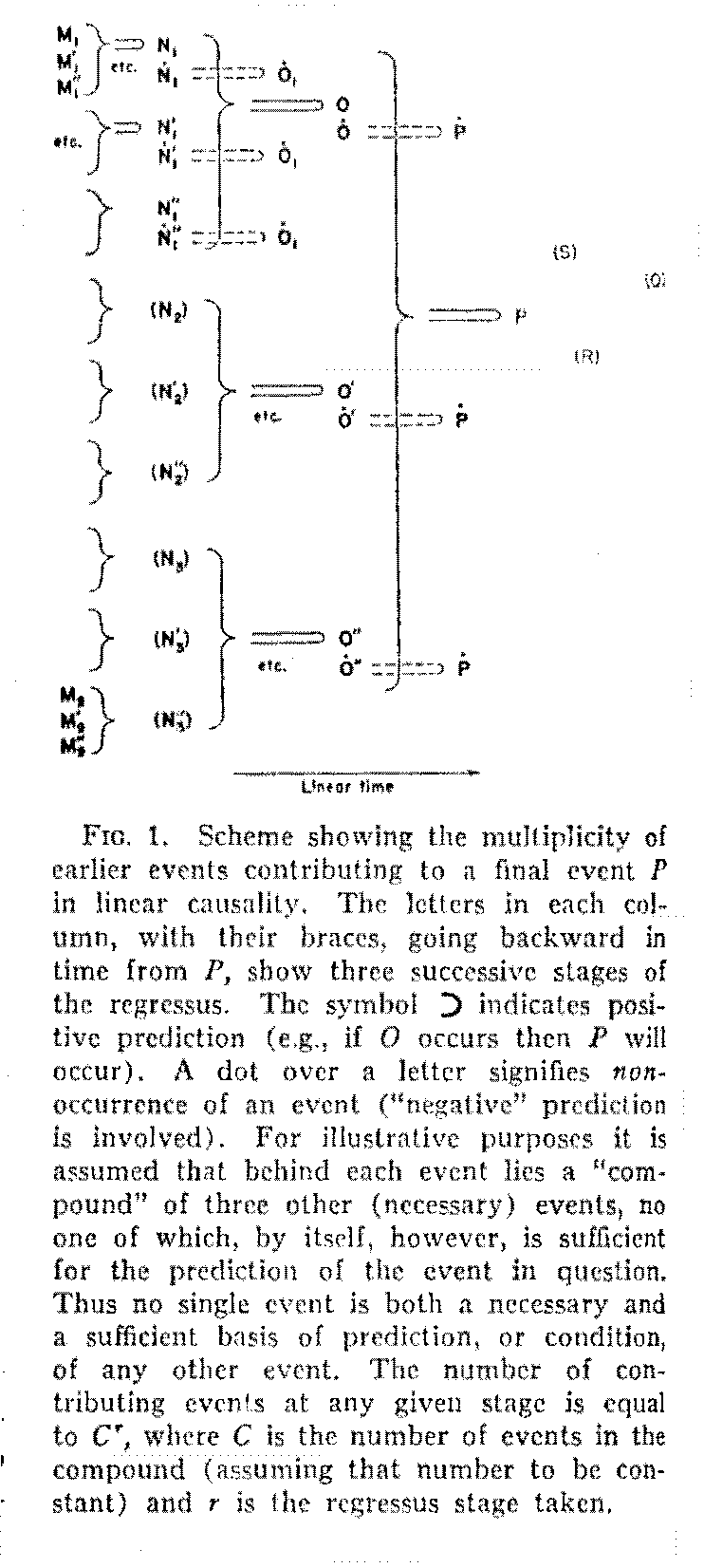
(287) is presented. The same analysis, of course, could be made with respect to the other objects, pitcher and glass, contacts with which were also a necessary part of the situation (Q, R, and S in Fig. 1). But now another difficulty arises. Each of these objects will have had its background pyramid series; and in order to produce the structure of behavior which we are considering the apices of these series must converge toward the interior of this particular dining room at a particular time when the boy also is there. How can we explain this convergence? We look in vain among the total antecedent events of the chair, the pitcher, the glass, and the boy, for any earmarks that will indicate a "destiny" of their coming together with the others at this time and place.
It might be argued that the boy's organism itself will supply the combining clue. The sequence is spelled out for us in the drive-and-stimulus-to-reaction chain of the mechanistic theories. But here again we shall meet with disappointment so long as we stick to the linear meaning of causality. First, we have the historical and environmental problem all over again in accounting for the 0's that lie in the boy's neural and muscular metabolism. But there is something more than that. There is built into the boy himself a kind of causal regressus pyramid. Neurologists have pointed out that as one proceeds (linearly) from receptor processes through central connections to effector units, a marked shrinkage in the number of elements or available pathways occurs. Many 0's are required for each ensuing P at every stage; and as one moves "backward" through these increasing sets of "multiple causes" the same sort of spreading effect is seen in the physiological regions as was noted in accounting for contacts with environmental objects. In terms of cyberneticsit is said that the loss of information merely in proceeding from neuron to muscle is 100 to 1 (3). And again, we have no way of describing by any causal series within the organism how the various elements or processes are integrated in the pattern of a single act. The structure simply "appears" among the ongoing elements as though it were not "caused" at all.
One further lesson can be gained from all this. We find that when we try to explain structure by temporal trains of causes and effects, we are usually faced by structure as an accomplished fact. The practically simultaneous excitations that existed in the boy's sensory cortex as he surveyed the possibilities of getting a drink of lemonade were all there together. The co-ordinations of separate movements by which he gained his end were also contemporaneous arrangements. Then too, as we looked back at the historical sequences outside the organism, the acts of human beings or machines by which the chair was transported, manufactured, and so on, these also were seen to be matters of spatiotemporal patterning. The behavior of one individual in any one of those aggregates was co-ordinated with and dependent upon the concurrent behavior of others. Patterns seem to flow not from linear trains of causes and effects, but somehow from patterns already existing. Structures come from structures; and in many cases the structures themselves, as wholes, seem to operate not sequentially but in a contemporaneous or concurrent fashion. Unless causality is already set in this "framework of structure" it becomes merely a pyramiding manifold of happenings without relevance to the structural problem. But when it is placed in such a setting is anything of importance added to the picture by the notion of causality?
III. TOWARD A GENERAL THEORY OF EVENT-STRUCTURE
It appears, therefore, that the attempt to explain structure through the customary time series of cause and effect is futile. Some other explanatory concept must be sought that will circumvent regressus and link up events in some kind of pattern. Explanations must lie in the approximate "here and now" rather than in the remote past. The only way to accomplish this seems to be to cut across the conventional and absolute "time stream." One can think of time as the duration occupied by the successive ongoing processes and events of a particular pattern that closes itself through a cycle of operation. Taking this idea as a clue, we shall begin the presentation of our proposed theory of structure by stating the following postulate: All structures of events have a self-closing or cyclical character. Instead of depicting the events of any aggregate, M, N, O, P, or P, Q, R, S, as a linear series, we shall always try to think of their occurrence as shown in Fig. 2. If P starts the series, the event succession returns to P, or at least to the region in which P occurs. If it returns to P, it may, thereafter, keep on
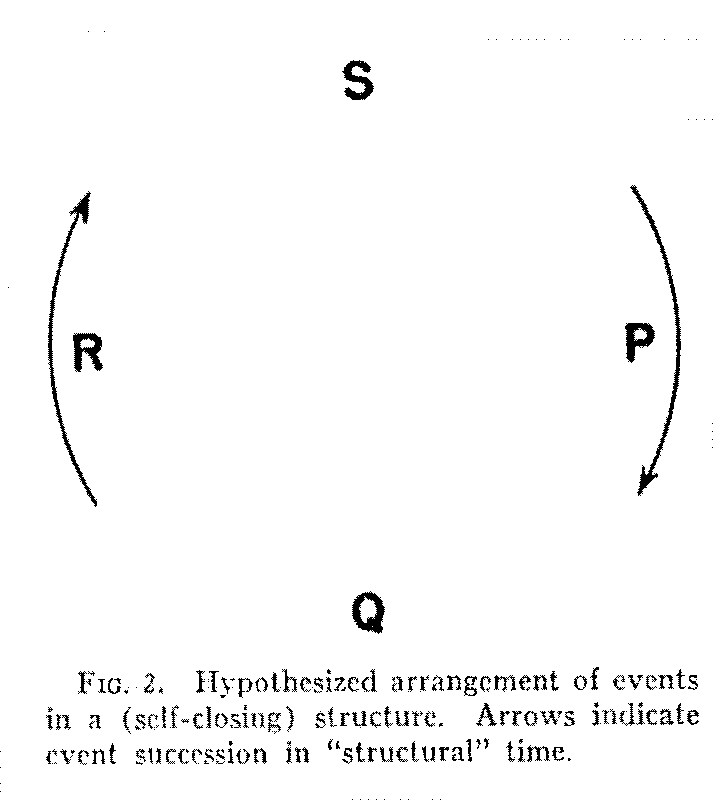
going in the same manner through repetitions of the cycle. If the cycle thus repeats itself, that would represent another "round" of "structural time." Time is thus always of the structure.
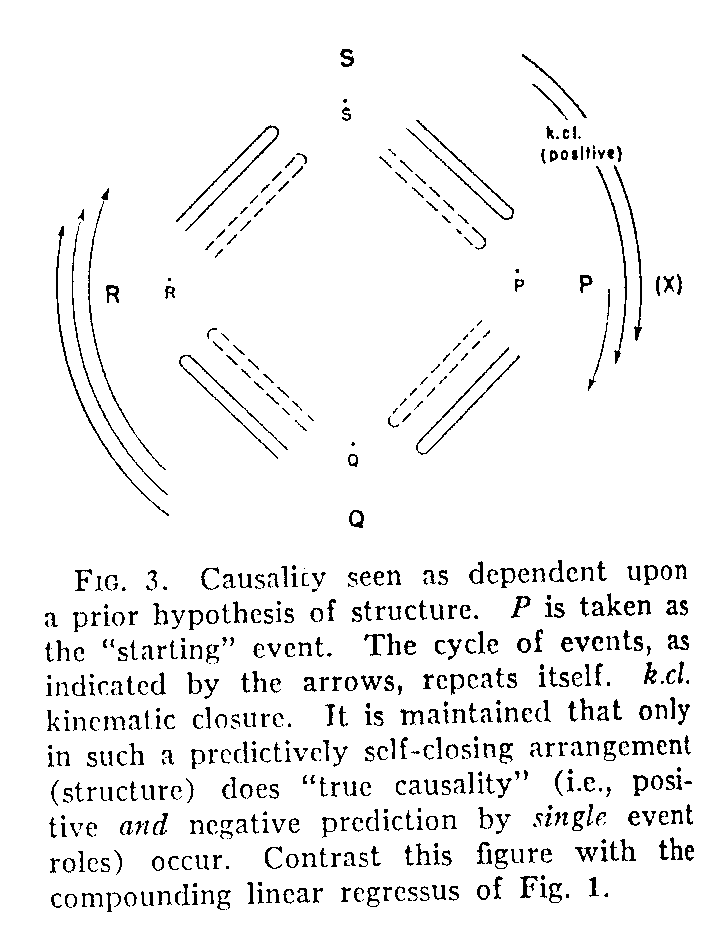
Though many such cycles of events may, of course, be connected by common events, regressus will be eliminated, first, because each structure preserves indefinitely its own characteristic pattern of ongoings, and secondly, because, though cycles can be linked indefinitely through space, their (repeating) operations may be actually "simultaneous" (that is, contemporaneous) in the linear meaning of time. The causality definition can here be re-introduced, if we wish, but this time in a structural rather than a linear setting. Figure 3 will illustrate this usage. The arrows suggest that this is a "repeating"cycle. We shall speak of the fact that the series returns to P (its starting point) as "kinematic closure" of the cycle (k. cl. in Fig. 3). In this case the closure is "positive" since it implies a continuation of the cycle. It
(289) should be recognized, however, that the reintroduction of causality, as shown by the symbols, is merely a device for semantic convenience. It does not contribute anything beyond the postulate of structure upon which it is here already predicated. P is the sufficient and necessary condition of Q, Q of R, and so on, only because of the postulated self-closing character of the pattern.
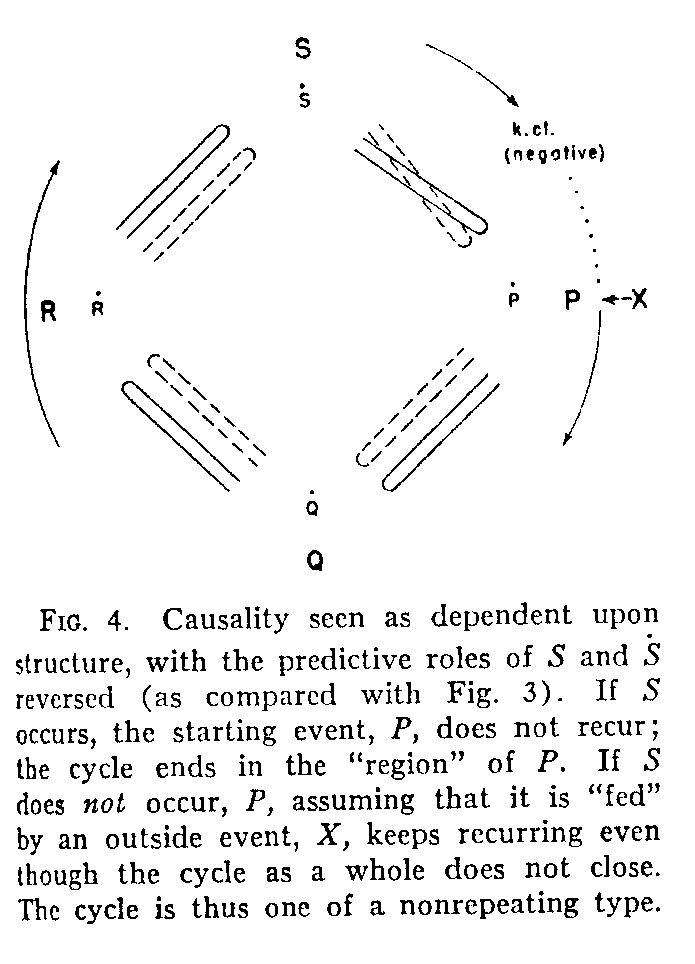
But in order to fit the facts of behavior there must be introduced a second logical construction, having a type of closure prediction different from the first. It contains, at the last event position of the cycle, a new type of causality statement that is the inverse of the old; namely, if S occurs, P (the starting event) will not recur, and if S does not occur P will keep recurring (tangency of the structure at P to some "outside" structure, X, is presupposed in the latter case). But again we note that it is the structural hypothesis that is fundamental, not the symbols or concepts of causality. This construction is shown in Fig. 4, and kinematic closureis here said to be negative. Such an arrangement typifies those cases in which the events of the cycle terminate upon a return to the initial region (non-repeating cycle). It may follow, in some cases, upon a series such as that represented in Fig. 3. An illustration of the latter condition would be found in food-taking behavior (by taking repeated mouthfuls) as the "hunger contractions," P (perhaps from blood-stream events), continue in the stomach. After a certain number of mouthfuls are taken, the situation represented in Fig. 4 would occur, brought about, perhaps, by a tangent cycle involving "nutrient" events in the blood stream. Another example of negative closure is to be found in the breaking of contact (event S) with a hot object, an event through which the initial event of stimulation (P) is prevented from continuing or recurring. If the reader wishes to generalize these schemes of positive and negative kinematic closure, he will find that they have a very broad application to behavior. It might, perhaps, be objected, that if we do not come back to an actual reoccurrence of event P (Fig. 4), we do not have a true closed cycle. We do, however, have a closed cycle in a fundamental sense, since, in order for P not to recur, there must be a change or "deflection" of some sort in the region of P that negates P's recurrence. For example, in the breaking of the contact of the hand with the hot object, the events do bring us back to a change in the state of affairs in the initial region.
We need one more addition to this purely logical stage of the model. Structures, wherever we take them in nature, probably never exist "in a vacuum." There is always "tangency" with other structures somewhere; and we can be sure that our structure R P Q
(290)
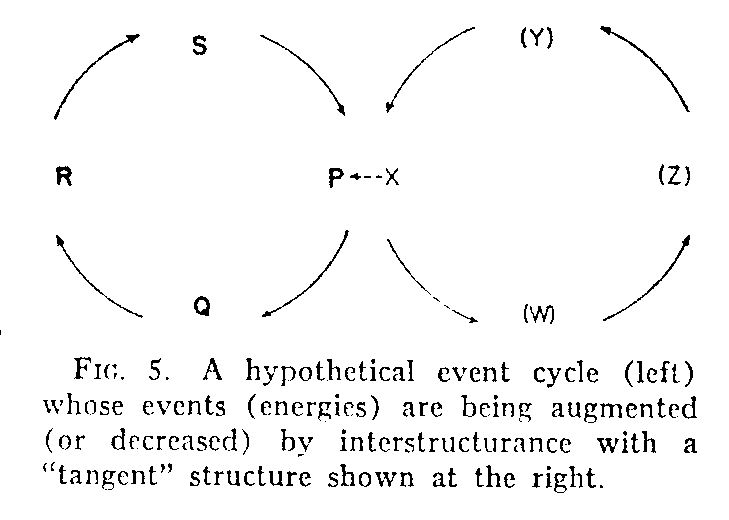
is not only operating at its own "proper" level or frequency of events, but is capable of receiving events (i.e., energies) from adjacent structures, or, perhaps, of losing energy to them by some kind of pre-empting of its elements. Let us represent such tangencies, with application to both the earlier nonrepeating and repeating models, by the symbolization of Fig. 5. X, which is an event (event role) of another structure, is not here regarded either as a sufficient or a necessary condition of P, in the sense of P as an event role. The position P would be the site of some events without the aid of the tangent structure. X provides merely an "energic reinforcement" of (or perhaps detraction from) the events occurring in structure PQRS. Linear causal regressus, in Fig. 2 through 5, has entirely disappeared. Aside from the structure PQRS, taken together with other structures (such as WXYZ) that may be immediately tangent to it, we have no interest in the nexus of events either in the past or the future. We do not care what the sources may be from which the contributing structure has, in turn, had its own energies supplemented, so long as the energies and the energic contribution of that structure to the main structure can be determined.
So much for the general format of the logical model. It was intimated above that the letters of the model are really event roles. The term "energies" was also used. These matters must now be explained. One of the defects of the notion of cause and effect, in addition to those mentioned, is that it implies that there is a specific event, O, invariably preceding and followed by another specific event, P. Empirical observation of event series, however, shows that such identifiable sequences of specific happenings do not invariably occur. We can say only that there is a certain probability that P will follow, and be preceded by, O. In fact, the occurrence of O (or of P) itself is a matter of probability dependent upon certain conditions. Instead of saying "if 0 then P," we might better say "probability of O, probability of P," and then add a third probability to express their joint occurrence or succession. Probability considerations, however, always imply that we must have a fairly large number of cases to observe. In order to determine probability or expectancy many events (or failures of events) and many successions or failures of successions must be counted under the classifications O and P and their interconnection. A further imperative reason for this pluralizing of the event concept within a role is the fact that we must make our model of structure general. It must fit all levels of nature (not just the macroscopic or molar level) or it will probably not fit any.
We might as well resign ourselves, then, to the necessity of treating events at the level of the microcosm (i.e., the most minute elements or happenings in nature) right at the start. And here, what has just been said of the indeterminacy of specific events and their succession applies with great force. There is, for example, no way of predicting that a certain minute particle, a, will collide with a certain particle, b, and hence there would be no prediction of a
(291) one-to-one series or closed sequence of such specific events. The best we can say is that for any particle there is a certain probability, through time, that it will be in a specified region and hence that it will be "available" there for an event of encounter with another particle. Whether one of these ultramicroscopic events will take place between two particular particles is "upon the lap of the gods." There is, however, a certain "probable density," or probable number of such encounters, that can in the aggregate be predicted to take place in a given region through a given time. If this is so, there is also a degree of probability that such (probable) encounters will occur in all the regions around the (hypothetical) structure. Cause and effect, in the usual sense, must therefore be replaced by a statistical treatment of the matter. Where the number of minute events recurring in a certain region is very large, so that they can be observed "macroscopically" or, as it were en masse, we say that "the event O" (at our level of observation) occurs. And if one of these (macroscopic) "events" regularly follows another in successive spatiotemporal regions of observation, we say "If O then P"–or, "O is the cause of P." This, however, is only a crude statement and one not at all suited for the careful study and explanation of structure.
The formulation of events in terms of probability holds, of course, for all the event positions labeled P, Q, R, S, and X of the preceding diagrams. (In Fig. 4 the probability in position P, following the occurrence of events at S, falls abruptly toward zero.) In order to apply these concepts it is evident that we must always regard P, Q, R, etc. in our logical model not as single definite happenings, but as indicating regions of space through time in which events may or may not occur. Theyare the "event regions" that are hypothesized as defining the structure. We must also be prepared to conceive the events in vast numbers in any region, and in ultramicroscopic as well as in macroscopic terms. But let us remember the further aspect of probability that must be incorporated in the design. Having dealt with the probabilities that events will occur in each of the regions P, Q, R, etc., singly, we now have to consider the probability that they will occur (with sufficient probable density) in all these regions of the self-closed structure taken together, that is, around the cycle, either simultaneously (if continuous) or in immediate temporal succession. As this probability approaches 1.0, it means that the structure in question is becoming increasingly clear and predictable. It is hypothesized that this is the phenomenon that takes place in both learning and perception.
Our second postulate, then, is as follows: The observed occurrence of a structure of happenings is dependent upon (a) the probability of occurrence of events in each of the (event) regions of the structure, the regions being taken singly, and (b) the probability of the joint (or successive) occurrence of events in all the regions of the struc-
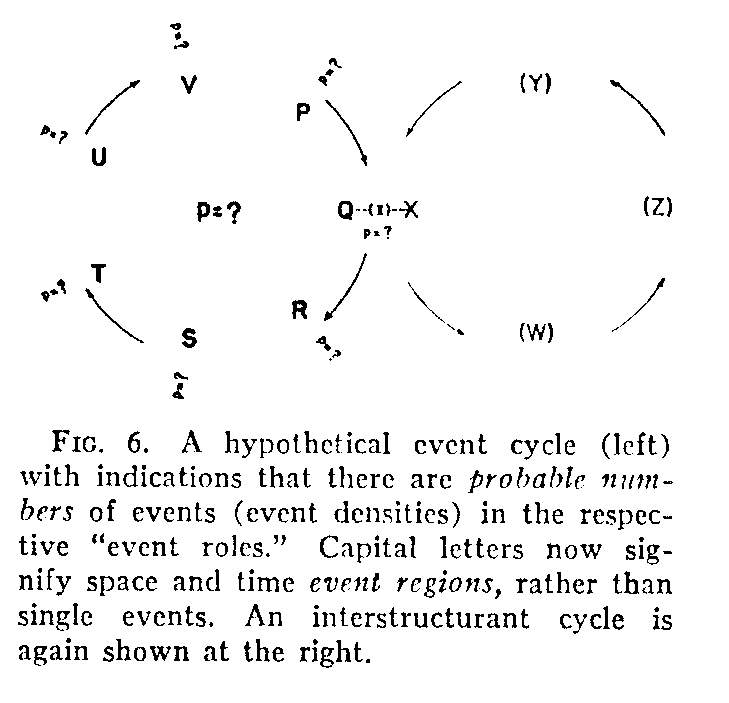
(292) -ture. This postulate is symbolized in Fig. 6 in which a larger number of regions is employed, the main structure under consideration being shown at the left. In this figure p indicates the probabilities within the single event regions represented by capital letters, and p the probability of the structure as a whole. As before, a contributing tangent structure is included for completeness. The I between Q and X represents an expected "interstructurance ratio" between increases of the events in the regions of structure WXYZ and those of the main structure. If the main structure is a food-taking behavior cycle, the contributing structure might be a cycle of events in the blood stream. Solid arrows indicate the temporal succession of events in the regions of the cycle.
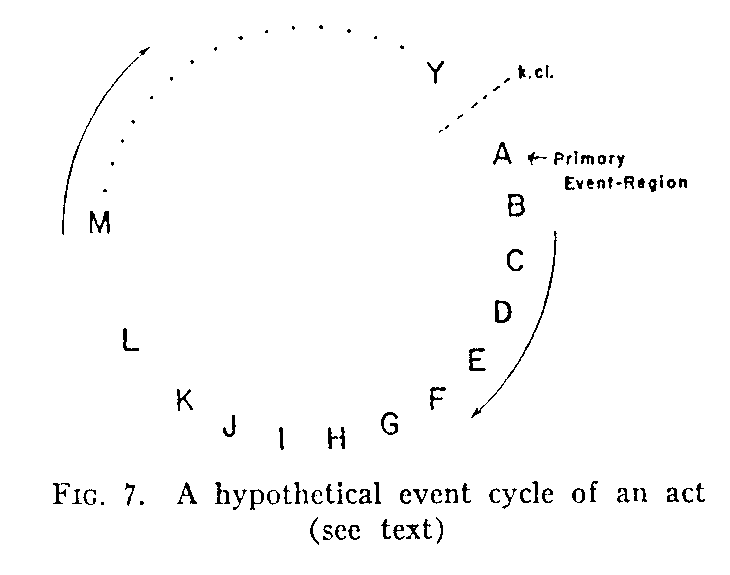
Before going further with the model, which is still, for the most part, only in a logical stage, let us make some direct applications to the organism. Again we shall discuss the example of the boy getting a drink of lemonade, but shall ignore the contributory cycle (at the right in Fig. 6) and consider only the main structure. Figure 7 presents, for this purpose, a cycle having a greater number of event regions. Probability symbols are omitted but should always be understood, both for the event regions and for the structure as a whole. Let us first establish a clearer
definition of the term "event." This we shall define solely in terms of an indivisible, all-or-none, happening, as, for example, in an encounter or collision where minute particle elements come together (or, in relativity theory, to "near points") and then go apart again as they continue on their courses. Events may also be the sudden breaking of contact between elements. The dichotomous states involved in ionization and chemical interchange could come under this general definition of events. Such a definition may not seem at first to fit happenings like action across synapses; but it is believed that, if conceived at a fine enough, ultramicroscopic, level, it can be considered appropriate. A single event, then, is a "dichotomizing," non-quantifiable, happening, and nothing more. Its representation on a spatiotemporal model would be merely a point. We shall sometimes, for convenience, speak of "an event" in the singular when we mean a large number of such events (that is, an event role); but it should always be remembered that the letters of the diagram (Fig. 7) represent event regions of space and time in each of which a large number of these elementary events occur, giving us, when they occur at a probable density of threshold frequency, "the event" as macroscopically observed. Thus, as we know, a large number of stimulation points are involved on the retina or the skin as the boy sees the pitcher and the chair or as he touches these objects. A large number of afferent-neuron excitations and cortical synaptic events are involved in the sequelae of these stimulations. A large number of muscle-fiber-activation events occur at the efferent end plates. Many molecules of liquid strike the boy's throat as he drinks, replacing the many that have evaporated from the throat membrane. Each of these pluralities can, of course, be regarded as
(293) the compounding of events in their more elementary status at the molecular or atomic level. It is useful to regard some one (or more) of the event regions of the model as a "primary" event region in that it represents the initial marked increase (or decrease) in events (energies) through tangencies with an outside structure. This procedure also locates the point of closure, which comes just before the primary event region (k. cl. in Fig. 7).
Let us now represent the event of "throat drying" or, more exactly, the region in which many microscopic eventsof tissue change occur as the body moisture evaporates, by A (Fig. 7). A, then, is the primary event region. Omitting vision and some other aspects for simplification, we can now assign to the other letters, as regions, approximately the following event roles: B, stimulation of receptor(s) in throat membrane (from the drying); C, excitation of afferent neuron(s); D, excitation of neuron(s) at synapses in the central nervous system; E, excitation of other neuron(s) at other synapses; F, excitation of efferent neuron(s); G, excitation of extensor arm muscle fibers at end plates (hand here moves forward toward the chair) ; H, contact of hand with chair; I, stimulation of proprioceptors and tactual receptors by this contact; J, K, L, M, etc., afferent, central, efferent, and muscle-fiber excitations (as hand closes on the back of the chair).
From this point on let us simplify matters by conceiving further elements of the series (dotted line) as representing other neural, synaptic, muscular, receptoral, and bodily contact events as the chair is placed in position and as the boy climbs up, takes the pitcher, pours a glass of lemonade, and tips the glass up at his (open) mouth. Eventually we come to an event (let us call it Y) at which the liquid encountersthe throat membrane and the "moistening" of the throat represents a partial negation (diminution of energies) in the "drying" events of the tissue. With kinematic closure at Y, then, we come back to the starting (or primary-event) region. Since the tissue-drying events are only partially reduced in number, a repetition of a part of the cycle will occur (positive k. cl.). This part, not distinguished in the diagram, could be charted as a "component" cycle involved in the taking of successive swallows. Finally, as the "swallow cycles" continue, event densities at A are reduced to a state at which the whole cycle is energically "in equilibrium." Events at A now cease to occur (negative kinematic closure) and with their nonoccurrence the remainder of the cycle is negated, at least in so far as the superthreshold level of "conduction" and overt action is concerned. It should be noted (though it cannot be explained at this point) that some of the event regions in the cycle may be more "readied" than others. That is, they may already have an event density approaching threshold, though the remainder are not yet at a probability stage in which the structure as a whole can appear. Continuation of the occurrence of events in the "readied" regions (see later) would guarantee their presence when needed for the total structure. (Many considerations that would need to be included in a full structural diagram, such, for example, as a coordinated cycle of mouth opening and [later] closing, have been omitted to simplify the illustration. Tangent "feedback" cycles of optical and opposed neuromuscular ongoings have also been omitted.)
There is still one feature that must be added to the logical model before it can be given its full physical or organismic significance. The events A, B, C, etc. of Fig. 7 are really connected.
(294) Is such connection only a matter of abstract joint probabilities, or is it "physical"? Theory and common sense both require the latter answer. If events represent encounters between minute (hypothetical) elements that collide or come to "near points" in their ongoings, then the only way in which such events can be connected is by the fact that one ongoing element, after it encounters its opposite, continues and makes an encounter with another ongoing element. To illustrate such ongoings in our example let us recall that water molecules travel in space as they "evaporate" from the throat membrane. Some kinetic feature is probably also present in the molecular activity of receptors, connecting stimulus event with afferent-neuron-excitation event. A neural impulse represents a whole train of minute cyclical ongoings (of ions) through and along the neural membrane, connecting the events of excitation at one end of the neuron with events of excitation at the other. The more grossly perceived ongoing of the hand as it raises the glass, represented at a microcosmic order by neural and muscular ongoing cycles, connects the event region of "glass grasping" with that of "glass tipping." The flowing (or fall) of the liquid is the descending portion of a gravitational cycle of ongoing and connects the events of displacement of the liquid as the glass is tipped with the events of the droplets striking the throat. In this way a connection of events is provided by each ongoing role. There is also a connection of the on-goings by events. There is, in other words, a structure of both ongoings and events. A kinetic or "motion" aspect must therefore be added to the elements of the model. To this task we shall presently return. Again we note, from the format of the model, that these several ongoings (which are in general themselves cyclical) and the events by which they are connected and which they connect form, when taken together, an over-all cycle (Fig. 7). And again, the numbers in which events occur in each of the regions separately, and therefore the probability of the behavior structure as a whole, are a matter of the (sub) microscopic probability density at the event regions.
It will be seen that regressus is completely eliminated from the model. All that is needed is that there be a sufficient space and time availability of ongoing elements at event regions necessary to constitute a structure. The pitcher of lemonade might have been on the buffet many hours, or it might have been there for only a thousandth of a second before the boy's eyes turned toward it or his hand encountered it; and it could have come there through any one of an indefinite number of pyramiding lines of "causality." These considerations are without significance for our present problem. The only thing that concerns us about the concentration of molecular cycles we call the pitcher and its contents is the probability that such a "concentration" will be present at a time and place that will permit encounters to be made with it by the "ongoing elements" of the boy's hand. Since, however, all events have a certain degree of randomness, this requirement makes room for "approximations." If, for example, the pitcher had been in another room, or had been available only just before the maximal drying (events) of the boy's throat occurred, the probability that a lemonade-getting-and-drinking structure would have occurred would have been less (though still not necessarily zero). And the same can be said for probable density at all the regions of the structure, including its tangencies with other structures, such as those of blood-stream events, which lie inside the organism.
It is unnecessary to ask what "makes"
(295) or "brings about" all these regional event probabilities and their concurrence in time and space. They are implicit in the empirical situation itself. If they were not, the structure (that is, the behavior) would not occur. No "field expectancy," "organizer," or "entelechy" is needed in a theory of event structure. We can think of the pitcher of lemonade, the glass, the chair, the internal systemic changes that occur in "thirst," and all other relevant situational features as "bounding conditions" of the lemonade-taking-and-drinking structure. These bounding conditions, which are themselves self-closing structures, increase, by imposing space-time limits upon the freedom of adjacent ongoings, the probability that the (bounded) ongoings of the cycle under consideration will come to events at intervening regions (including synaptic areas) with a density above the macroscopic threshold; and in so doing they help to bring about the self-contained and self-closing structure of the (bounded) behavioral act. The implications of this conception for a new and more comprehensive theory of learning are evident. The notion of the probability density of a structure's occurrence under given bounding conditions might be substituted for such earlier notions as sign gestalten, "stimuli" linearly evoking "responses," strength of associative S—R linkages, and the selection and fixation of neural pathways. The difference between continuity and noncontinuity learning may be merely a difference in the shape of the curves of distribution of the increasing probable structural densities of the act as the experimental situation is repeated, the curve in each case being plotted along a continuum of structurizations or "trials" with experimentally imposed bounding conditions that are different in the two cases.
Let us now return to the problem of representing the motion of ongoing elements in the model. In order to supply this feature, the ongoing must be represented as curves, each suggesting continuous motion; for it seems probable that at the minute levels of nature particles are in continual motion and that their motion is cyclical or vibratory. Moreover, nothing ever starts from a position of ascertainable "absolute rest" or proceeds to another point of absolute rest. In fact, if we are to get away from a purely static conception, points in space and time are definable only as the points of conjunction between ongoings or motions. Let us try to diagram the situation, at first, without any consideration of where the ongoings start or of their ultimate destiny. Let us also avoid trying, for the moment, to link the model too closely to neurophysiological considerations. Figure 8 shows six ongoings (broken lines i to v, and r) with event regions between adjacent ongoings. Evidently we must assume that there is something in each case that "goes on." Without trying to be more specific, let us postulate, for the purpose of the geometry of the model, that it is, in the last analysis, a "continuance-head" (or particle?) of the smallest conceivable magnitude. (If the diagram were adapted to our present example, the compounded, or higher order, ongoing elements would represent such features as ion cycles in neural impulses, muscle-fiber molecular lengthenings and shortenings, flowing of the liquid, and so on.) The "event-connecting" segments of these ongoings occupy the central portion of Fig. 8. These ongoings must, of course, be conceived in plural number for each ongoing role; and we know, in fact, that this is actually the case. In any act of behavior, after many points are stimulated on a receptor surface, many neural impulses travel, as it were, "in parallel," many cortical fibers are involved, many
(296)
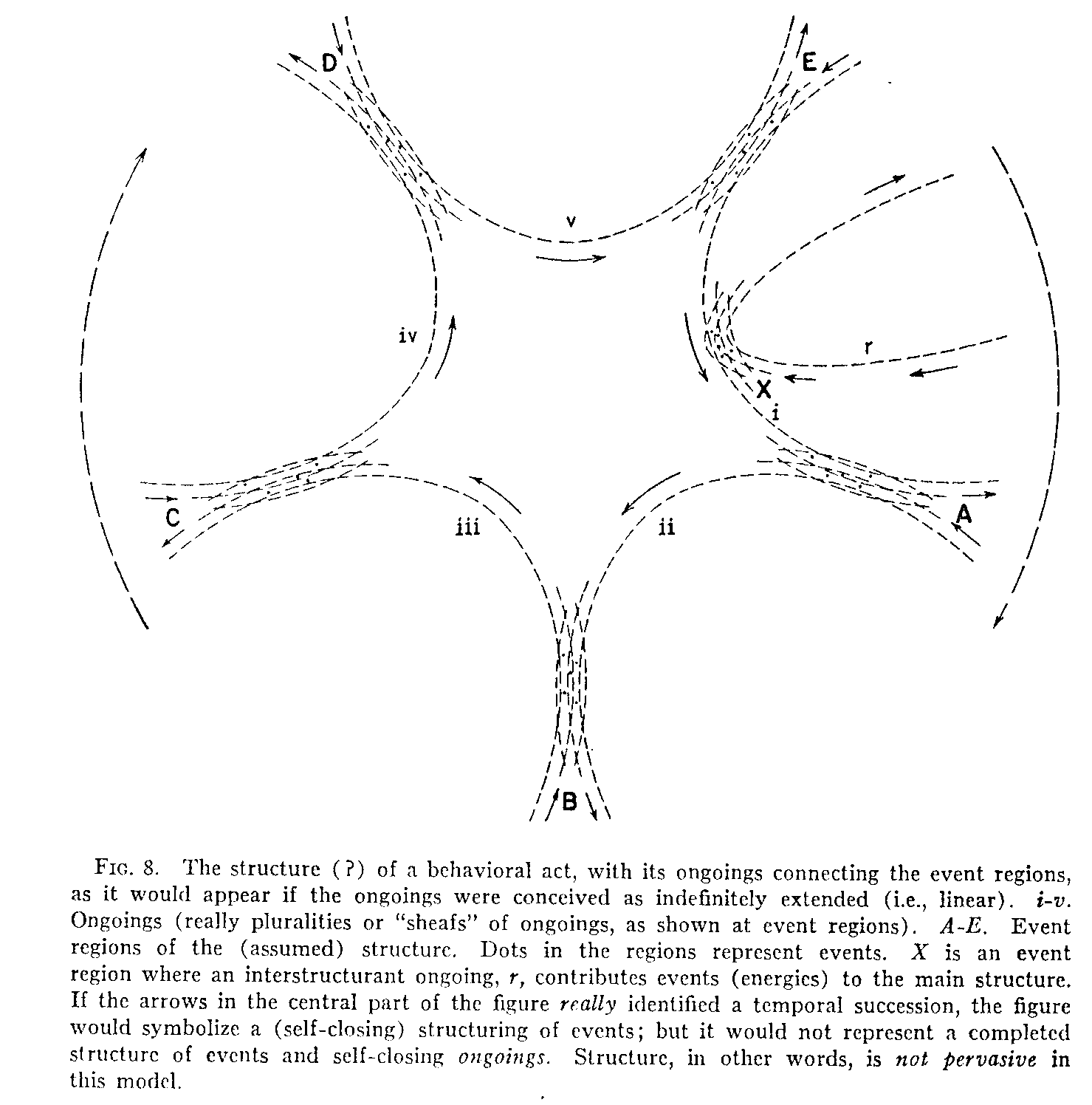
muscle fibers contract in their common role in a single effector movement, and so on. Note that this feature is suggested in Fig. 8 by the duplication of the lines for the ongoings (shown only in the areas of the event regions). Events between these multiplicities of ongoings, whose probable density or numbers in the several regions underlie the structural probability of the act, are indicated by dots. Ignoring ongoing r and region X for the present, we shall regard ongoing i and region A as our starting point. The short solid arrows indicate the direction or sense of the ongoings; and they show a temporal clockwise succession of event occurrences in regions A to E and back to A, as indicated by the longer broken arrows at the margin of the figure. We now have a cyclical structure of events (but of events only), connected by continuous ongoings which themselves are not structured but extend (small arrows
(297) at the periphery) from an indefinite past into an indefinite future. Let us see if this construction is satisfactory.
At least three provisions must be made for any structural model of behavior: (a) It must accommodate itself both to relatively stationary and to "successive" patternings. In some structures, as, for example, in perceptions of objects, all parts of the object seem to be perceived at once. On the other hand, many typical structures of behavior have a cyclical succession of happenings (as we have shown, for example, in the case of the boy and the lemonade). (b) In order to meet the latter requirement there must be some suitable arrangement for the timing of the ongoing elements so that the events (regions) will occur in proper order. (c) Many behaviors not only occur in sequential arrangements but are sustained, in the sense of a repetition (of their complete cycles), through time. This feature, which is called steady state, requires a continual input contribution of events (energies) from some explicable source.
An examination of Fig. 8 shows that the construction there presented does not meet these requirements. Time coincidence of ongoing elements in an event region and time sequence of the successive regions are shown but not explained; and in order to account for them we would probably have to invoke some special "organizing agency." "Static" or simultaneous event structuring could be accommodated if we consider that, instead of separate "volleys" of particles coming to events in the region, we have a continuous flow of particles along the course of each ongoing. Events would then be occurring in the five regions (A . . . E) in practical simultaneity. The situation so represented might be equivalent to an "equilibrium" of the structure. If we should wish to turn the picture into a kind of succession, we could do so by adding an "input source" in the form of another ongoing stream (r in Fig. 8) which comes to an event region (X) with one of the ongoing streams of the main structure. If the increases in numbers of events introduced into the cycle at X are passed on from one stream of ongoings to another, we would then have successive increases of density in regions A through E, and thereafter, under conditions of positive kinematic closure, around the cycle repeatedly. We can suppose that there will be some sort of output tangency to keep the state in balance, so that the full energies continually being added to A from X are not passed back from E, via i, to A, but only a portion of those energies. This interesting explanation, which may be called a theorem of "conduction," gives a basis for steady state. So far so good. But a difficulty arises in these explanations both of equilibrium and of steady state. Some continuous source for the ongoings (i.e., ongoing elements) is needed in both instances. Where, for example, does ongoing r get its supply? Either we must think of these sources as the ongoing lines themselves, extending from an infinite past, a conclusion at odds with the temporal self-containedness of phenomena, or else we must suppose that they are derived, for each of the unclosed ongoings in the figure, from tangencies with other, more remote, sets of (unclosed) ongoings. In the latter case we begin to slide back into the old multiple regressus.
The difficulties here encountered can be summarized by saying that we have been trying to build a self-closed structure out of materials that are themselves unstructured. One cannot make a true structure out of open-ended lines that merely "butt against" one another as in Fig. 8. Structure must be pervasive if it is to exist at all. It must be composed of units (in this case, on-
(298) -goings) that are themselves self-closed. We need, therefore, to suppose that the six ongoing roles of Fig. 8, instead of extending out indefinitely in space through time, have a curvature throughout their course and return upon themselves. Could we say, perhaps, that the ongoings follow the curvature of the continuum of space-time?
Without trying to elaborate the last proposal we shall pass at once to a new and final design in accordance with the idea just expressed. It represents merely an extension of our first postulate (self-closedness) down to the lowest orders of the microcosm. For cartographic convenience only six subcycles of ongoings and six event regions will be used. Actually, of course, there would be a very large number since the model must be conceived, ultimately, in microcosmic terms. In Fig. 9 we have shown this structure, in principle, as 1, together with out-structural tangencies with two other structures, 2 and 2a, affording an input or added increment of event density, and an output, respectively. The legend will recall the meanings of the various symbols, and the earlier organismic details given for the boy-lemonade episode in connection with Fig. 7 (or any other behavior by which the reader might wish to test the model) will supply illustrative content. In applying the construction of Fig. 9 it should be remembered that there is no limit upon the number of subcycles of which the structure under consideration can be composed. We now have a consistent theoretical model of a structuring of events, in this case the structure of a behavioral act. It consists (see structure 1) of a set of subcycles of ongoings and a cycle of events (event regions) between, and provided by, the ongoings—a cycle of cyclical ongoings and events. Though the evidence cannot be here fully presented, but must rest with the specifications of the microcosm previously mentioned, the writer believes that the gross and finer facts of neurology, physiology, and environmental contacts will justify the use of such a model for the description of behavior. It is also consistent with structural principles to assume the existence of "higher" orders of structure, that is. of structures that are composed of cycles of cycles of cycles, and so on. For example, conceive a larger cycle made by joining a number of cycles such as 1 in Fig. 9. Structure can thus be pervasive and can provide an explanation of the various levels or "hierarchies" of nature. (As the reader will see, this was impossible with constructions like that of Fig. 8.) Such higher orders, for example, might describe the collective or "social" structurings of the behavior structures of individuals; and such a description could well replace the present ambiguous and unsatisfactory term "group."
The three requirements listed earlier for a structural model are all met by Fig. 9. Equilibrium or a "static" structural condition is achieved under certain conditions by the fact that the ongoings of each of the subcycles (see smallest arrows) return again after one event region to the region where they had been just previously. With a continuous flow of elements around each of the ongoing subcycles, a virtual simultaneity of events would occur throughout the structure.[2] But whenever a sudden increase in the probable density of events is given through a tangent in-put structure (2 in Fig. 9), the equilibrium of the structure is disturbed; and this increase, beginning with the primary event region, that is, the re-
(299)
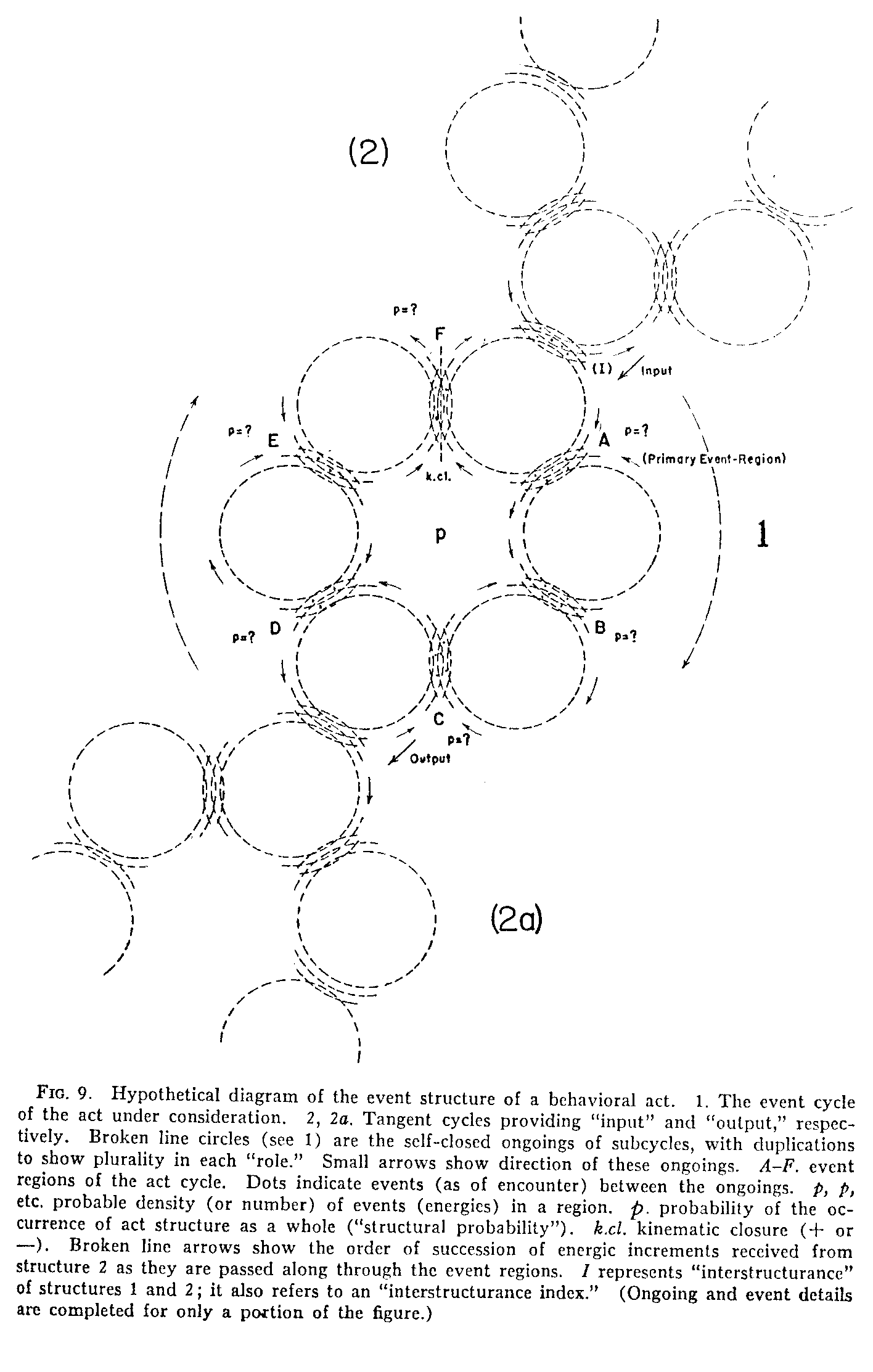
(300) -gion first increased, is displaced around the cycle of event regions (broken arrows). Such a situation occurs in the full phasic sequences of a behavioral act and perhaps even at subthreshold density levels. With repeated rounds of the event cycle, should these occur, we would have a steady state. The problem of coincidence timing is solved by the reverberating character of the sub-cycles, which, with particle-elements continually ongoing, provide a continual availability for events. Succession in time could be guaranteed, in the sense of a succession of energic increases, by the passing along of increments from one event region to the next in the steady-state condition mentioned above. There is now no difficulty in providing for the source of the energic units of the cycle, or of the energic contributions made to the structure by adjacent structures. For we are not faced by a regressus to indefinite origins. The subcycles themselves, and the cycles of the tangent structures, continually possess availability for events in the immediate present by the self-closing and repetitive character of their ongoings. And we need to consider only the event cycle of the behavior in which we are interested plus the cycles that are immediately adjacent to it.
The task outlined at the beginning of this article has now been, at least in part, accomplished. It has been shown that by laying aside linear models and linear causality, and by passing over into a logic of structure supplemented by probabilities, we can arrive at a fairly clear conception of "another type"of natural law. The conception of such a law is essentially "geometric" rather than quantitative. Our statement of this (hypothesized) law, however, has been as objective in principle and precise in reference as statements of laws that are based on "abstracted" measured quantities. The writer maintains that the proposed paradigm is general for all acts of behavior and that it even suggests a unifying bridge across the "hierarchy of the sciences." Event-structure theory, though it includes quantitative considerations, nevertheless rests upon a foundation that is basically nonquantitative. Consider, for example, such concepts as the self-closedness of ongoing, the forms of kinematic closure, the indivisibility of an event, and the compounding of structural orders. No statements of dimensions, counts, or measurements can convey the full and essential meaning of these conceptions. The system is essentially a geometry of ongoings and their interrelations at "event points." In short, it is a theory of structural kinematics. But at the same time a place for quantities and covariational laws is provided. For quantities are probably related, in the last analysis, to energies; and energies can be represented, as we have shown, as structured potentialities for numbers of events. Hence the entire conception embraces also a theory of "structural energics" or "structural dynamics." It is important to note, however, that a rational place for quantitative laws could not have been provided without the (nonquantitative) structural kinematics.
The writer believes that the event-structural paradigm will be found to be applicable to all organismic phenomena at the biological and physiological, as well as at the behavioral, level, and that it will apply also to collective or social aggregates. Obviously the theory, as here proposed, is only in a pioneering stage. The account here given is also merely a general outline from which many details have had to be omitted. Many questions arise for which answers must later be provided; and a large amount of work, both
(301) experimental and theoretical, will be needed in order to arrive at a true appraisal of its validity. A further, though not a final, step in the theory's presentation, in which some of these questions are answered and additional properties and principles of structure appear, will be undertaken in a forthcoming volume (1). The theory will there be approached and exemplified through the facts and theories of perception.
IV. QUANTITATIVE ASPECTS OF EVENT-STRUCTURE THEORY (STRUCTURAL ENERGICS)
It is hoped that nothing that has been said will be construed as a failure to realize the importance of quantitative methods in the work of science. The quantitative and nonquantitative aspects of investigation should proceed together. An attempt has therefore been made to deduce some quantitative hypotheses from the over-all model, and, through the aid of students and associates, these hypotheses have been tested experimentally. Space will permit only, the briefest description of this work.
The major hypothesis, thus far, has been concerned with predicting the amount of energy in a structure (cf., for illustrative discussion, structure 1 of Fig. 9). Such energy or probable event density is conceived under two aspects, the "autonomous" or "proper" energy of the structure, which is called the energy of "structurance," and the energy that is contributed to it by other structures in "constructurance" with it, such, for example, as that shown at 2 in Fig. 9. There may be few of these or a great many, but all must be considered. Such contributions constitute the energy of "interstructurance" or the "interstructurance increments" provided to the main structure by its surrounding tangent structures,or "manifold." But the structures of the manifold may, in some cases, be "antistructurant," rather than constructurant, to the main structure. That is, there may be some kind of kinematic "deflection" which deprives the main structure of energies by decreasing its probable density, so that, instead of having the two structures increase in energies together when the tangent structure receives increases from its manifold, we may have a decrease in the energies of the main structure as the tangent structure is increasing. The contribution to the main structure from manifold structures (e.g., from structure 2 in Fig. 9) will, in such cases, have a minus sign. The constructurant relationship represents instances of facilitation in the biological, behavioral, and social realms, while the antistructurant relation represents alternation, inhibition, or "conflict." Furthermore, it is conceived that such additions or subtractions of energy proceed by constant (kinematically determined) ratios to increases in the manifold structure. This ratio (increase in the main structure divided by the attendant increase or loss in the manifold structure) is called the "index of interstructurance" of the manifold structure to the main structure. The interstructurance index (suggested as applying at I in Fig. 9) is specific to the pair of structures concerned, is limited to unity, and may be either positive or negative. (Actually it should represent a function expressed by a curve showing the relationship of the two variables.) The "output" quantity of the structure (for example, to 2a in Fig. 9) can be neglected in this problem, since our objective is to find the amount of energy which is available in the main structure at a given (present) time, either for self-maintenance of the structure or for being passed on to adjacent structures. Hence the total amount of energies of a structure, so
(302) defined, at any given time, is a function of (a) its proper or "structurance" energies, which represent a sort of mean of its operation through time, or, if one prefers, a "homeostatic level," and (b) the sum of the interstructurance increments (or decrements) that are being received from its manifold. It is believed that these increments or decrements are given by the structurance energies of the manifold structures concerned, the latter, however, being first weighted, respectively, by their indices of interstructurance with the main structure. In the symbolism of the diagram (Fig. 9) this total amount of energies corresponds to the total number of dots in all the event regions of structure 1 (remembering that these have been augmented, or detracted from, through interstructurance with manifold structure 2 at I).
The generalized equation that has been derived in this manner from the postulates, kinematic concepts, and definitions of the theory is stated as follows:
E1 = f(S1 + S2 I2→1 + S3 I3→1 . . . + Sn In→1),
where the subscripts indicate different structures (1 being the main structure under consideration), El is the total energy of the main structure, S is the "proper"energy or structurance value of a structure, and I is the index of interstructurance of a (manifold) structure to the main structure as shown by the subscripts and arrows. Structures 2 to n represent all the structures of the manifold; and the summation is, of course, algebraic. This equation is known as the structural-energics (or structural-dynamics) formula. In using the formula, manifold structures considered on logical grounds to be very low in S or in I are usually omitted as having no appreciable value in the summation. Should the value of the equation turn out to be negative, El would not represent "negative" energies occurring in structure 1, but presumably (positive) energies that were being expended in a structure or structures antistructurant to 1. The manifold of structures (shown to the right of Si in the equation) can be broken down into various classes or types, and the contributions of these types, separately, to the dependent variable, E1i can be determined. For example, in predicting the intensity with which an attitude is held by an individual (energics of an attitude structure), as El, three types of manifold structures have been used, viz., personality-trend structures of the subject, small "face-to-face" collective structures into which his own behavior is structured, and his larger organized, or institutional, structures. The total summation, as provided by the equation, is hypothesized as giving a fairly accurate prediction of strength for the attitude concerned .[3]
The testing of adapted forms of the equation has thus far been carried on by simple correlation procedures involving El and the manifold summation only. Methods of measurement for S and I, and sometimes for E, have been limited to subjective scaling, but with carefully prepared forms. The actual "energies" implied in E and S have thus far had to be inferred from the reactions on response forms or in an experimental situation. The equation has been tested (or tested in part) in nine independent investigations, largely at the structural orders of personality and social psychology, and representing cases from the fields of propaganda, attitudes, personality characteristics, job adjustments in industry, insight, learn-
(303) -ing, and custom behaviors of American males. In all but one of these investigations (an early one in which it now seems that the hypothesis was not adequately stated) significant correlations, ranging approximately from .20 to .80, were obtained. Worthy of note here are the variety of structures whose total energies were to be determined, the considerable number of independent raters often employed for determining the different variables, the very large number of manifold structures whose increments entered into the summation for each subject in most of the experiments, and the fact that these interstructurance increments were either positive or negative and hence involved subtraction as well as addition of energies in computing the predicted E. The consistent experimental support given the hypothesis in the face of these complex conditions seems surprising and would tend to suggest that, although it was developed in a highly general frame of reference, or perhaps because it was so developed, the theory does accommodate itself to the quantitative facts of human behavior.[4]
V. SUMMARY
The adequacy of quantitative laws and the common practice of thinking in terms of linear cause and effect, as methods of dealing with the universal problem of structure, are questioned. The need of approaching the study of structure in its own right, and by independent and (at the start) nonquantitative concepts, is stressed; and a general conceptual model of the structuring of ongoings and events is presented and illustrated in the field of behavior. The combined headings of structural kinematics or geometry (nonquantitative) and structural energics (quantitative) are here found useful. An equation for the latter is developed, and experimental findings thus far obtained in its testing in the field of psychological phenomena are briefly discussed.
REFERENCES
1. ALLPORT, F. H. Theories of perception and the concept of structure. New York: Wiley, in press.
2. HULL, C. L.,HOVLAND, C. I., ROSS, R. T., HALL, M., PERKINS, D. T., & FITCH, F. B. Mathematico-deductive theory of rote learning. New Haven: Yale Univer. Press, 1940.
3. McCULLOCH, W. S. Why the mind is in the head. In L. A. Jeffress (Ed.), Cerebral mechanisms in behavior. New York: Wiley, 1951. Pp. 42-57.
(Received April 9, 1954)