The J-Curve Hypothesis of Conforming Behavior
Floyd Henry Allport
I. DISTRIBUTION ON A TELIC CONTINUUM: THE J-CURVE HYPOTHESIS
Franklin H. Giddings once made a statement to the effect that, if we could sufficiently reduce the prevailing temperature, we would find practically everyone going about with his coat collar turned up about his ears. This remark of the founder of "pluralistic behavior" contains not only a profound truth, but a vital suggestion for research. It points out a field of objective phenomena which can be agreed upon, isolated, and 'measured. All that is needed is that we ask further questions which are suggested by the statement quoted. First, what is the degree of temperature at which this universally similar behavior will occur, and what determines it at that point? Secondly, will all the people respond by turning up their collars? If not, what proportion will so respond? And what about those who do not? Will they do other, and perhaps lesser, acts toward the end of keeping warm?, If so, what actions, and what proportions will perform these acts respectively?
Not only Giddings, but other social students, have regarded their field as dealing properly with social norms or modes of agreement. Their work has consisted in discovering, defining, and describing such modal points of conformity as the content of a generally accepted attitude, a folkway, a custom, a tradition, a convention, or an institution, or such societal tendencies as "public opinion," mass action, imitation, social forces, pressures, and culture patterns. Social solidarities are also presupposed in various forms of human
(142) engineering, from nationalistic movements to working-class propaganda and organized charity. This emphasis upon uniformity, though legitimate for certain purposes, is inadequate for a statement of society in terms of human action. We want to know not only the abstract mode, or position of conformity, but the entire "lay" or distribution of human behavior upon the act in question and the factors contributing to that distribution. Until we know this, we shall never know the relevance of the conventional pattern to individual needs; nor can we predict either the need or the likelihood of change.
A few years ago, Dr. Richard Schanck was applying certain scales for measuring the attitudes of people in a rural community (near Syracuse, New York) toward symbols representing their town, their associations, and their institutions.[2] He expected that he would find the usual bell-shaped, normal probability distribution of these attitudes, and hence could readily use their median as an index of measurement for the community. To his surprise, however, many of his distributions were skewed far to one side, some of them so completely as to be one-sided in slope. The mean or median of a distribution of this sort did not seem to possess so much significance as the fact that the distribution was one-sided and steep at a particular point. There was consequently much difficulty in trying to find a way to describe his data in the conventional, statistical terms. It then occurred to the present writer that this might be the very nature of the distribution of those behaviors which make up social customs and institutions; in other words, that conforming behavior is something to be described not so much in terms of a norm or index, as in terms of an entire distribution. Since that time the writer has been testing and developing this hypothesis in studies at Syracuse University. Further data have been added by a number of students and colleagues. Dr. Schanck and Mr. Milton Dickens, in particular, have made valuable contributions. The purpose of this paper is to assemble the data now on hand and to attempt a precise statement of the hypothesis involved.
To understand the basis upon which our data have been collected, it is necessary to think of a series of units, or positions, along what we may call a telic continuum. This is a continuum of purpose.
(143) It deals with the question of "how much of" (or how fully) a certain purposive, meaningful, prescribed act is carried out in practice. Such a continuum is also concerned with the objective to be gained by the concerted action of many individuals, an objective commonly recognized, and one toward which we may expect a fair degree of conformity in action. For example, we have employed a continuum dealing with the degree of obedience to traffic signals, such as boulevard stop signs, red lights, etc. The underlying purpose of such signals and regulations, in the minds both of those who made them and those who obey them, is the securing of safety while driving in traffic. The question of to what extent, or how well, one obeys the traffic rule can be determined only by interpreting what one actually does in the traffic situation in terms of how fully that act fulfills this underlying purpose. The positions[3] on our continuum represent recognizable degrees in which this purpose is fulfilled by respective degrees of performance of the prescribed act. Thus stopping completely before the crossing at the appearance of the red light would be the maximum degree of fulfillment. All who stop at the red light lie in this first position of maximum satisfaction of the purpose of traffic safety through complete obedience to the rule. The next recognized degree is slowing down considerably, but not stopping, before the red light. This act represents a smaller degree of fulfillment of the purpose through a lesser degree of obedience to the regulation. Slowing down only slightly is our third scale position. It represents a still smaller degree of obedience and fulfillment. The fourth and last position is going ahead without change of speed, an act which represents an entire disregard of the signal and no fulfillment whatsoever of the common purpose of safety in motor traffic.[4] These four degrees of speed of motorists at red-light crossings have been found to be
 (144)
(144)
 (145)
(145)
(146)
 (147)
(147)
(148) readily distinguished and recorded; and their accuracy of discrimination has been checked by chronometric methods. Our telic continuum, it will be seen, is one of the amount of fulfillment of the purpose of the common or prescribed act; and the points on the continuum are recognizable classifications of the fulfillment, arranged in order.
The data with which we are now concerned are shown in connection with the left-hand, solid black figures on each page of the accompanying charts. The heights of the black columns indicate the number of cases falling upon the different positions of the telic continuum. Throughout the charts, solid as well as shaded figures indicate the distribution of observations actually made.
Figure 1, from the work of Milton Dickens, shows the distribution of motorists on the continuum just described. The number of cases is 2114. The conditions involve the reaction to boulevard stop signs rather than red lights. The reactions were also taken only in cases where there was traffic coming at right angles to the direction of travel of the motorists concerned ; so that a double incentive to stop was presented in the possibility of a collision and the presence of the stop sign. The data were gathered in two large cities. It will be seen that on the first position, that of complete stop, there were 1594 cases, or 75.5 per cent, of the entire number. On the second position, that of proceeding very slowly, there were 462 cases, or 22 per cent. On the third position, slowing only slightly, there were 47 cases, or 2 per cent. On the final position, proceeding without change of speed, there were 11 cases, or .5 per cent. The distribution is thus steepest on the position representing most complete obedience and fulfillment of the purpose of traffic safety, and decreases steadily to the position representing the least fulfillment recognizable, or no fulfillment at all. It is further to be noted that the decrease is less with each succeeding interval. The curve which is here hypothetically suggested, if one follows it upward from its lower extremity on the x axis, is one of positive acceleration. It may be compared roughly with a reversed letter J (without the tail of the J being turned up).
Figure 2 (also from Dickens) is compiled from the behavior of 102 motorists at a busy intersection in Syracuse, New York. The stimulating circumstances were both red signal lights and a policeman; but there was no cross traffic. Cars immediately behind other
(149) cars, that is, those whose drivers had no choice but to stop, are not included. Here we see the same tendencies, but in more marked degree. Ninety-four per cent stopped completely, 3 per cent proceeded very slowly, 2 per cent slowed slightly, and 1 per cent went ahead without change of speed. The reverse-J-distribution, with the maximum number of cases on the position of complete fulfillment and the minimum on that of no fulfillment, is suggested.
Figure 3 (from data recorded by Miss Miriam Gartner) shows the distribution of the behavior of 124 pedestrians when confronted by red lights at street crossings in a city where laws governing the response of pedestrians to signal lights were in force. Here the continuum has three indicated positions: completely stopping and waiting before the red light, looking to right and left and then proceeding against the light, and going ahead without looking. The distributions on these positions are 92, 26, and 6 cases, respectively. These results conform in general pattern with the distributions pictured above; but there is an insufficient number of positions to test the J-curve theory adequately.
Figure 4 (reproduced by courtesy of Mr. Hawley S. Simpson)[5] indicates the lengths of time cars were left parked in city regions where the parking limit was one-half hour. The ordinates represent the number of cases in thousands, and the base line a scale of successive half-hour intervals. Again our telic continuum represents degree of fulfillment of the purpose to relieve traffic congestion by degree of adherence to a rule. We may regard the behavior of the motorists of the cars represented in the first column of the figure as conforming fully with the purpose of the traffic regulation, that is, as "within the law"; while the motorists of the cars in the succeeding columns are to be regarded as fulfilling it in less and less degree. Here again we find our J-shaped pattern, descending from maximum conformity by generally diminishing increments of difference to the end of the distribution.
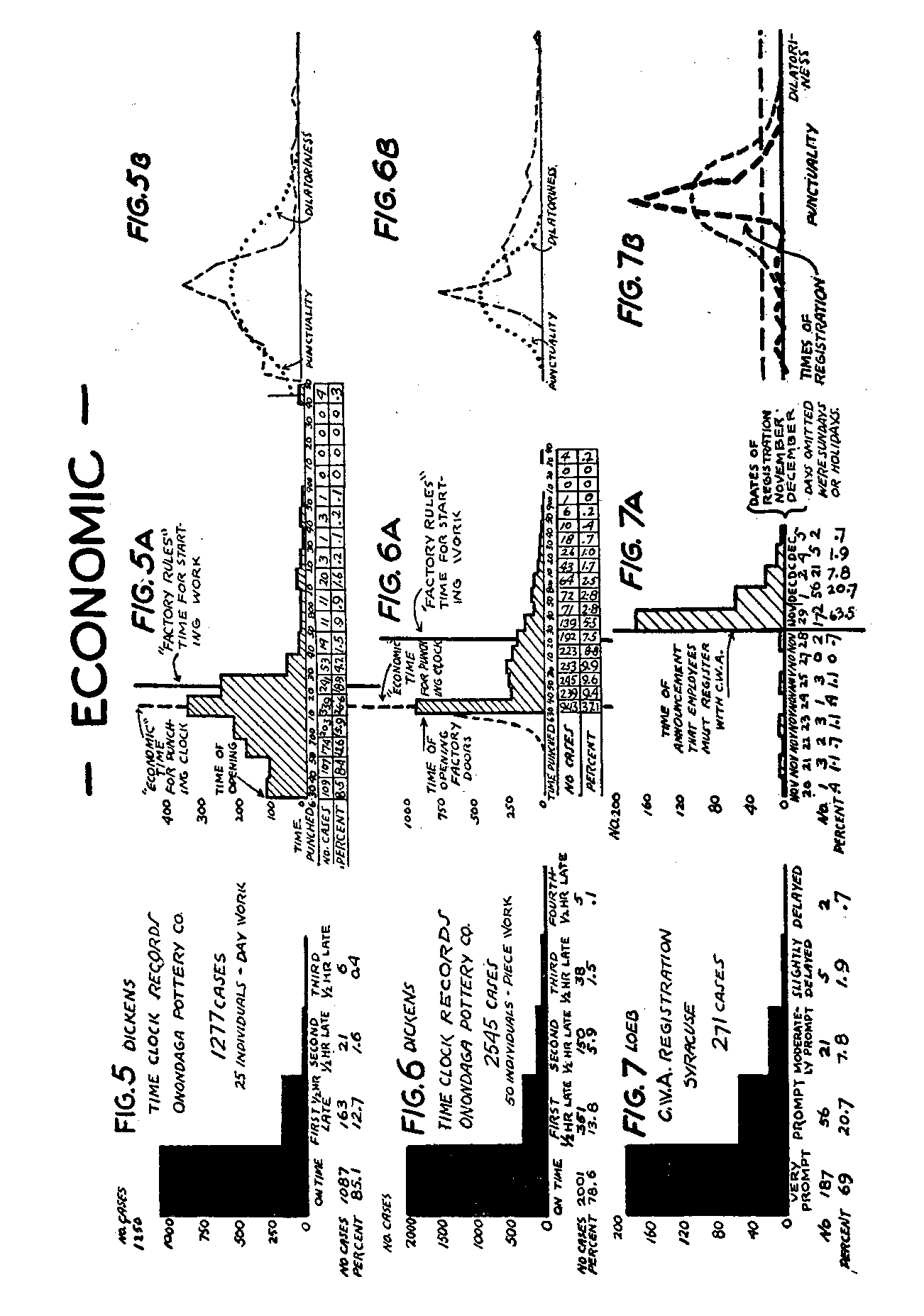
Let us turn now from the field of governmental regulation to industry. Mr. Dickens hit upon the ingenious scheme of consulting the time-clock records of a factory for measurable evidence of behavior distribution. Figure 5 represents his summary of the time-clock cards of 25 male employees of the Onondaga Pottery Company, Syracuse, New York, over a period of about 13 weeks.
(150) The subjects were day-workers. The data recorded are the times at which the clock was punched in the morning. There are 1277 reactions in all. The time at which work began was 7:25 A.M., and those who were late were penalized by a deduction of pay according to their lateness. We have constructed a telic continuum extending from "on time" (or complete conformity with the employers' purpose of efficient factory management) toward the right by successive degrees of half-hours of lateness. Mr. Dickens found that 85 per cent of the reactions were "on time," 12.7 per cent were within the first half-hour of lateness, 1.6 per cent were within the second half-hour of lateness, and the remainder, .4 per cent, were within the third half-hour. It will' be` seen that' this array conforms to the J-shaped pattern of distribution.
Figure 6 is a graph of similar data gathered by Mr. Dickens, comprising 2545 reactions of 50 male piece-workers at the same factory during the same period. The percentages on various steps range by successively diminishing amounts from 78.6 per cent "on time" to .1 per cent "punching-in" during the fourth half-hour of lateness. The piece-workers, therefore, follow the same tendencies in their distribution as the day-workers.
Figure 7, contributed by Miss Dorothy Loeb, shows the reactions of 271 employees of a city welfare department when told it would be necessary for them to register with the Civil Works Administration for continuation of their employment. A few cases are included in the left-hand column who had already registered before this announcement was made. Our telic scale here may be considered as ranging from very prompt compliance, that is, registration on the same day, to registration four working days later. The degrees of compliance corresponding to these one-day scale intervals may be described as very prompt, prompt, moderately prompt, slightly delayed, and delayed. The number of cases falling on these steps are 187, 56, 21, 5, and 2, respectively. Again we see a positively accelerated J-curve, ranging from maximum conformity or fulfillment of purpose to the least fulfillment.
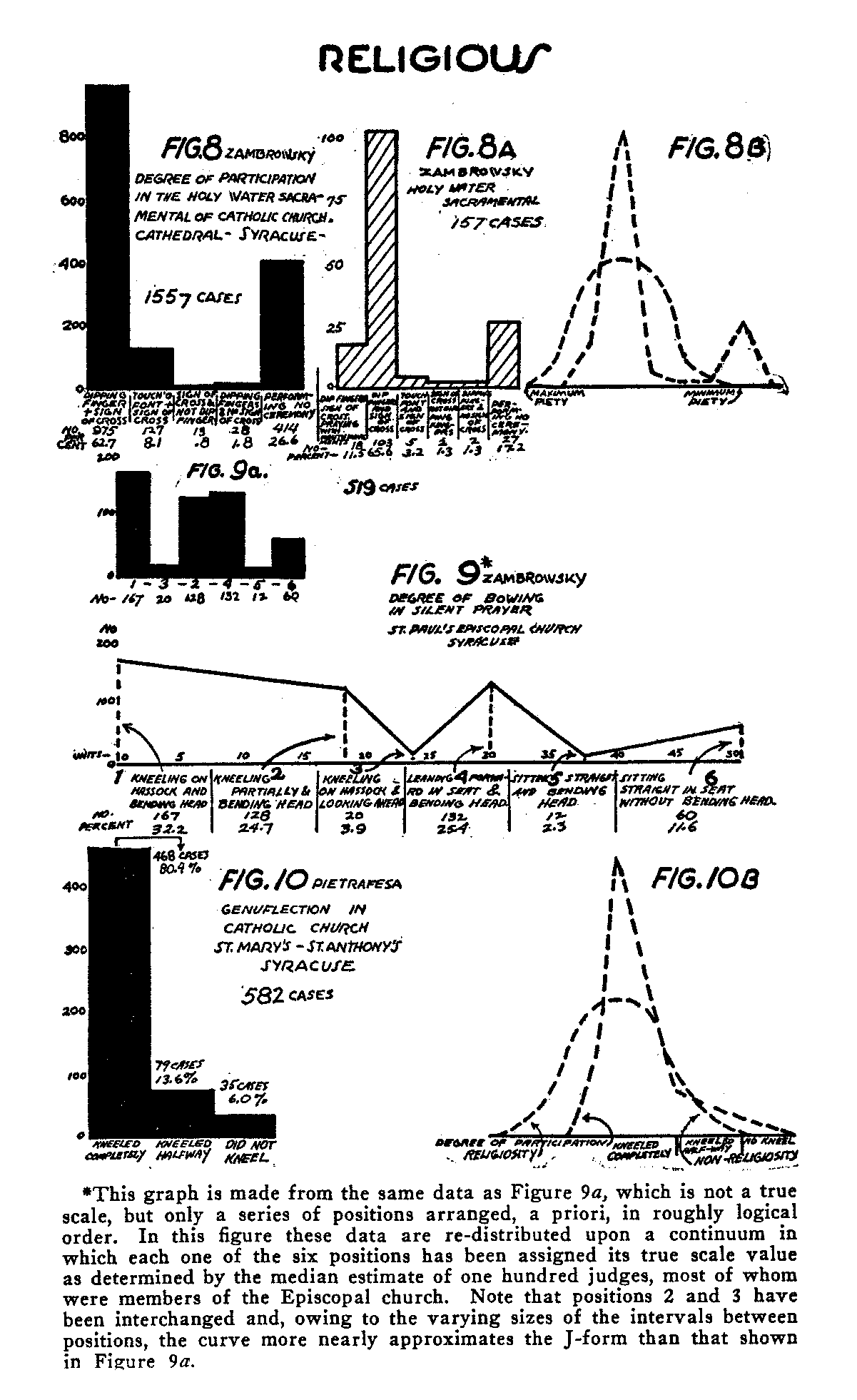
Figure 8 takes us from the economic field to that of religious behavior. Miss Basia Zambrowsky has studied the behavior of Catholics at the Cathedral in Syracuse, New York, in stopping before entering to dip their fingers in holy water and snake the sign of the cross. The data are compiled from a number of masses on
(151) different Sundays. The continuum positions and distributions are as follows: Complete compliance in carrying out the purpose of the sacramental, that is, dipping the fingers and making the sign of the cross, is the first position at the left.[6] Of a total of 1557 cases, 975, or 62.7 per cent, gave this reaction. The second position, expressing the purpose of the ritual in slightly less degree, is touching the font (but not dipping the fingers) and making the sign of the cross. One hundred twenty-seven subjects, or 8.1 per cent, made this response. The third recognizable degree of fulfillment is making the sign of the cross without either dipping the finger or touching the font. Those who fell on this position numbered 13, or .8 per cent. The' fourth position is dipping the finger but 'not making the sign of the cross. Twenty-eight, or 1.8 per cent, reacted in this manner. The final category, which does not properly belong to the continuum of conformity at all, consists of walking in without performing any ceremony whatsoever. This includes 414, or 26.6 per cent of the subjects.[7] A glance at this figure reveals the same general tendencies as previously noted, with certain exceptions. The distribution upon position 3 is lower than it should be to accord with our theory of the positively accelerating J-curve, and the final category, non-participation, comes up considerably higher. The increase upon the last position may show a tendency toward division among Catholics in regard to this ritual, or it may suggest the presence of some non-Catholic visitors. If we formulate our J-curve hypothesis, however, only upon the basis of those who, in some measure, conform, and exclude the others, the distribution upon this last step may be legitimately ignored.
Figure 9a (small graph), also contributed by Miss Zambrowsky, represents the behavior of Episcopalians with reference to the custom of bowing in silent prayer upon taking their places in their pews.
(152) The telic continuum represents the degree of satisfaction of the purpose involved in this ceremony, which is construed as putting the participant in the proper mood for the service to follow. The recognized degrees range from the usual practice of pulling out and kneeling upon a hassock and bowing the head upon the arms (position 1), on the one extreme, to taking one's seat without any bowing whatsoever (position 6), on the other extreme. Position 2 represents a rather unusual form of observed behavior, consisting of kneeling upon the hassock but looking straight ahead instead of bowing the head. Position 3 represents kneeling partially, that is, with knees on the hassock and body also resting on the edge of the pew, and bending the head. Position 4 is sitting, but leaning forward from the hips and bowing the head. Position 5 consists of sitting with the body upright in the, seat, but bowing the head. The total number of cases observed was 519. Here we see a general tendency to diminish in proportions as we go toward the noncomplying end of the continuum. The positive acceleration in this case, however, does not seem to be present. Non-conformists (the final position) in this distribution present a class similar to those among the Catholics who failed to perform the holy-water ceremony and may be neglected in our formulation of the pattern of conformity.
In Figure 9a, as in some of our other figures; it is obvious that we have no proof that the sizes of the intervals between the continuum positions are equal. And if they are unequal, we do not know what the true intervals should be. We cannot even be entirely certain that these positions are arranged in correct order. We have, in other words, no scale upon this continuum. In order to determine what the true order and scale values of the positions should be we have, in the case of Figure 9a, prepared instruction sheets and enlisted the support of a group of judges. Our instruction sheets contained the continuum positions mimeographed as strips; and we requested each judge to cut these strips out and paste each of them along the edge of a standard-sized sheet of paper, according to the place he thought it should occupy in relation to the other continuum positions. His standard of judgment in each case was to be the degree in which he felt that the particular manner of kneeling or bowing satisfied the purpose of the ceremony, namely, that of putting the participant in a fitting mood for the service to
(153) follow. Estimates of this sort were obtained from a hundred judges, most of whom were members of the Episcopal church. The distance of each strip, as placed by each judge, from the left-hand edge of the paper was then measured in 1/4ths of an inch, and the frequencies plotted for each strip in cumulative fashion. The point where each of these cumulative curves cut the 50 percentile line (that is, the median of each distribution) was taken as the proper scale position of the statement in question.[8] Laying out these intervals along a base line, the data of Figure 9a were replotted, and the result is shown in Figure 9. It will be seen that positions 2 and 3 are interchanged from their former relationships; and this fact, together with the increase in size of the intervals adjacent to the first and last positions, gives the distribution slightly more of the J-form than it possessed in Figure 9a. It is still conspicuous, however, as compared with the other figures in its discrepancy from the true J-form. We shall discuss the factors entering into this distribution more fully later.
Figure 10 represents the degree of kneeling in two Syracuse Catholic churches, as shown in data compiled by Mr. Arthur Pietrafesa. The combined data comprise 582 cases. The positions respectively represent complete kneeling, partial kneeling, and no degree of kneeling. Since only two of these three positions represent degrees of conformity, the theory of the J-shaped distribution of conforming behavior cannot be said to be here fully exemplified. These results, however, are not contradictory to it. The percentages on the three positions, respectively, are 80.4, 13.6, and 6. In this distribution there is no terminal increase in the number of nonparticipants.
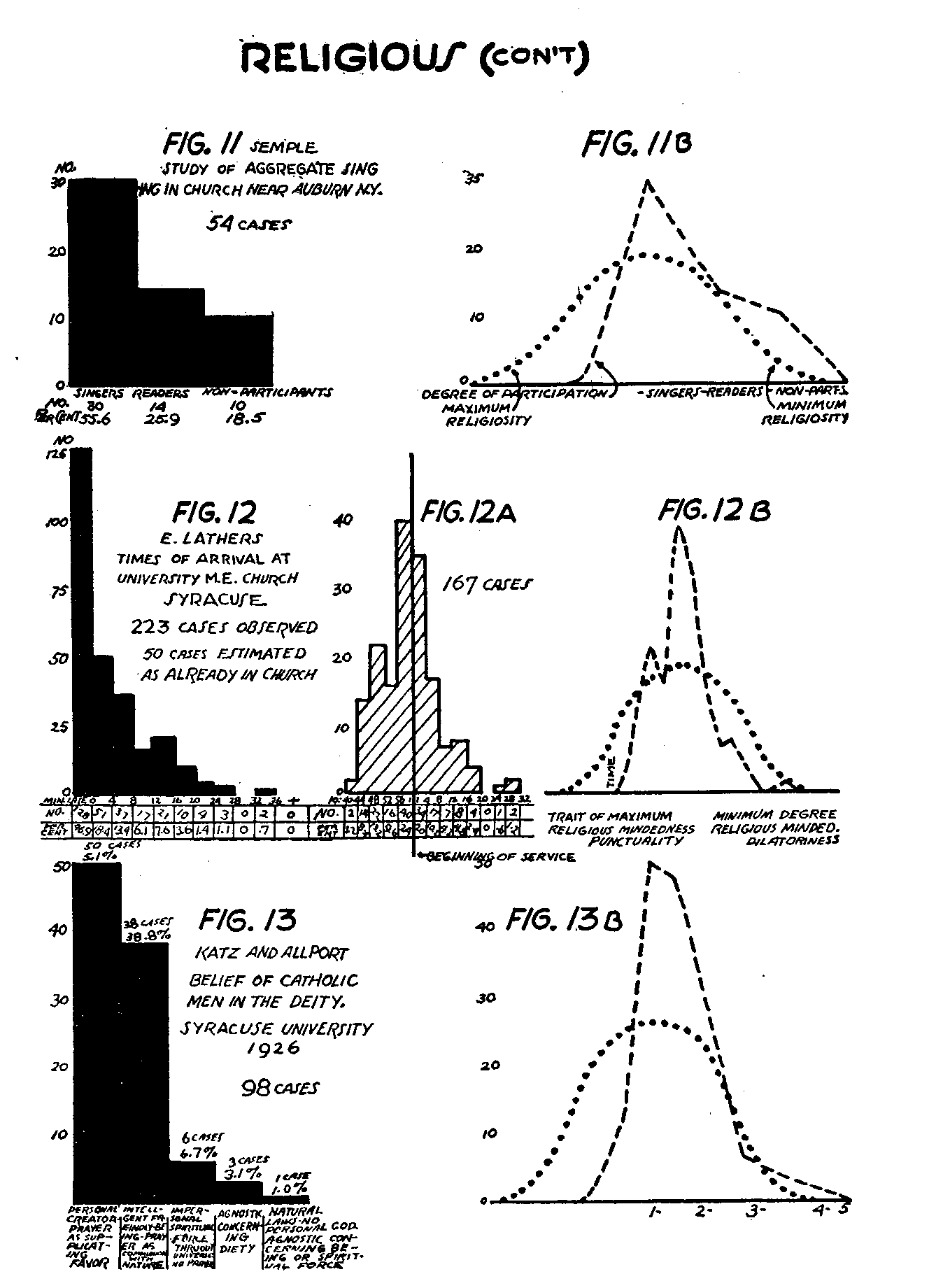
Figure 11 is derived from so few cases that it probably is not statistically reliable. The data, collected by Mr. Robert Semple, are arranged upon a continuum dealing with participation in congregational singing. The position at the left represents singers, the middle position those who did not sing but read (or followed the hymn with their eyes) as it was being sung, and the right-hand position, those who took no part whatever. Here again there are too few positions of conformity adequately to test the J-curve theory.
(154) The number of observations totaled 54; and the numbers in the columns from left to right are 30, 14, and 10 respectively.
Figure 12 is similar to the time-clock records of arrival at a factory. The data, compiled by Miss Eleanor Lathers, represent observations of the time when 223 individuals arrived at a certain church on a Sunday morning. The figure shows, in the left-hand column, those who were "on time" ; and on successive steps to the right are indicated the proportions of those who were late (that is, who arrived after the service had begun) by successive intervals of four minutes. The tendency of distribution again clearly resembles the J-form.
Figure 13, reproduced from Student attitudes, by Katz and Allport, indicates the distribution of the beliefs regarding the nature of the deity among male Catholic students at Syracuse University in the year 1926. The position at the extreme left represents an Old Testament conception of the deity as personal creator and ruler, while that at the extreme right states that natural laws prevail, that there is no personal deity, and that we should be agnostic regarding spiritualistic notions of the universe. The proportions of the cases, ranging from complete compliance or conformity at the left to the least conformity at the right, again exhibit, with the exception of one column, the usual J-shaped distribution. This interpretation, of course, rests upon the assumption that the view of God as a personal creator and ruler fulfills more adequately than any other view presented the purpose of the Catholic doctrine approved for members of that faith.
From the data so far obtained, it therefore appears that when we plot the distribution of behaviors in a situation where individuals are said generally to conform we find the following condition: Rarely, if ever, do we find that all the individuals conform completely. A varying number conform only in partial degree. The proportions of these are distributed in a diminishing fashion as we proceed to the wider variations from the modal act. Their degrees of diminution, ''moreover, become 'less as we proceed out toward the deviating extreme. In all our observations, with the exception of Figure 9a, no cases have been found in which the use of the telic continuum to record degrees of performance of the common
(156) act failed to give us at least a fair approximation of the J-form of distribution.[9]
In certain fields of behavior, a number of individuals may be found who do not conform in any degree. These will vary in number according as our sample includes more or fewer who have been under the influence of the common stimulating pressure. In traffic ordinances, for example, practically every motorist in the city is potentially affected, and there is material punishment for non-conformity. In the taking of holy water on entering church, only certain classes of people are affected, and there is no punishment for non-conformers. The occurrence or proportions in our samples of these groups who "do not belong" are, so far as our present techniques of prediction are concerned, quite fortuitous; and we therefore limit our hypothesis to the distribution of those who in some recognizable degree do conform.
Two objections will probably be raised at this point. First, some of the continuum positions we have been using are purely a priori, logical values, rather than empirically or experimentally determined steps. There is no way of knowing that the intervals between the positions of such a continuum are of equal psychological value. We do not know, for example, whether touching the font and crossing one's self is equidistant between dipping the finger and crossing and simply dipping the finger, or whether it should be nearer to the complete ceremony than to the dipping. Nor do we know that going very slowly past a red traffic signal is just halfway between a complete stop and slowing up slightly. So far as it affects our results the force of this objection is admitted. It
(156) will be necessary before a complete proof of our hypothesis is obtained to construct and apply scales by psychophysical techniques, perhaps similar in principle to those of Professor Thurstone.[10] The full effects of constructing and using psychophysical scales in investigations of this type remain yet to be seen. The psychophysical scales thus far constructed by other investigators have been based mainly upon an affective or ideational, rather than upon a telic continuum.
There is clear proof, however, that in a number of instances our J-forms of distribution could not have been the result of using continua of unequal position intervals. It should be pointed out that five of our continua were true scales, that is, they contained positions between which the intervals were equal in the physical and exact sense (Figures 4, 5, 6, 7, and 12). And it is in these cases that we find the J-curve of distribution not only present, but present in the clearest and sharpest form. In view of this fact the force of the objection that some of our continua do not represent true scales becomes considerably reduced.[11]
The second possible objection is that we have not taken small enough intervals between our continuum positions and have not extended our records far enough on the left. For example, in the investigation of length of parking time (Figure 4), some cars were probably parked for less time than the half-hour allowed by law. If, therefore, we took units of five minutes rather than one-half hour and
(157) plotted the number of cases, we should find not a J-curve, but a curve with two slopes, having a pointed, steep, and skewed character. Or, in stopping before the red light, some motorists may put on the brakes more quickly than others and come to a stop behind the point which the law actually requires. This fact, if represented upon an extended scale of time units, would again give a two-sided, skewed distribution. Again, employees may not only come to a factory on time, but ahead of time; and so on. This objection, though fully conceded, is not in any sense a detraction from the principle as we have stated it, but only a prelude to a fuller consideration of our data as distributed upon a non-telic continuum, a task to which we shall presently turn. It should be noted that, so far, while we have in some instances used physically measurable and equal empirical units, we have spoken only in terms of a telic continuum, that is, in terms of the degree of fulfillment of the purpose of a common rule. From this standpoint it is legitimate to group together all the cases where the behavior is "more than" that required by the rule, as simply "within the law," or as satisfying completely the requirement. Though some may conform more quickly or vigorously than others, the content of one's act cannot be more conforming than conformity itself, that is, than
(158) the modal act. We have a right, therefore, to construe the data as falling upon such purely telic continua and to formulate the principle of the J-distributions which results, so long as we make it clear that our formulation applies only to distributions as plotted upon a continuum of this sort and indicates only degrees of compliance with a prescribed standard.
Before attempting a formal statement of the J-curve hypothesis, we are brought finally to the necessity of a clearer definition of the field with which this hypothesis deals. We have spoken in our preceding discussion of three necessary factors. First, there must be a clearly recognizable, unequivocal purpose to be achieved by the behavior in question. Second, there must be some kind of law, rule, regulation, or code, in the language of which one may find stated the "proper" or required mode of behavior by which this purpose is to be achieved. This prescribed act is that which we have placed as the extreme left-hand position of our telic continuum. Third, a fairly large proportion of the population studied must do this prescribed act.
A little thought will convince one that these three requirements are not arbitrarily chosen, but are all necessary and are closely interwoven. In the first place, a purpose is necessary because acts which people perform in common, such as customs and institutions, are never sporadic, random activities like the reflexes of a newborn infant. They are meaningful adjustments to definite situations. There must always be some end to be achieved before a public rule can be made or even implied. The end may not always be for the interests of the greater number; but it is at least a recognizable purpose of some person or persons. Secondly, it is necessary that there be a rule defining the expected behavior before the purpose can have any widespread or practical significance. Before we can have conformity of action, we must have a standard to which people can conform. The term "rule," however, should be given a wide construction. It may be taken to indicate a mode of behavior prescribed, established, or defined in any one of a large number of ways, providing the prescription is definite. The only requirement is that somewhere, at some time, the rule is definitely stated or is capable of being stated in such a way that the majority of people will recognize the statement as authoritative or as universally accepted. Examples may be found in codified law and statutes, in
(159) canon law, in books of church doctrine and ritual, in governmental or industrial regulations, in school and college catalogues, in manuals of etiquette, and in any of the accepted phrases by which customary behavior is described. Usually, the rules are most precisely referred to and formulated by heads of "institutions" or reputed authorities on institutional procedure. Thirdly, there must be a fairly large proportion of behavior in compliance with the rule, because, in situations where only a meager minority conform, it will be likely that the influences tending to produce conformity, such as education, punishment, and social approval, will be so weak as to be outweighed, in different instances and in varying amounts, by other considerations. In this event no very constant proportions can be expected to fall upon the various degrees of the continuum. If a traffic ordinance, for example, exists merely on the statute books and is very loosely enforced, all talk both of the law and degrees of conformity to it are purely academic matters without counterpart in actual behavior. Almost any proportions of the varying degrees of compliance with this ordinance may be expected according to the time and local circumstances. A rule is a rule in an effective, behavioral sense only when a fairly large proportion of people obey it. How large a proportion must obey it is a question to which we shall presently return.
It is not only the fact of a fair degree of conformity which gives societal behavior distributions a character conducive to their prediction, but the common purpose and the rule itself are indispensable aids in the making of a scale by which the distribution can be described. Before we can have degrees of deviation from the rule, we must have the rule itself; 'for the deviations are merely other, or lesser, acts which are included, in a meaningful way, in the complete performance of the rule. For example, bending the body slightly is an act which is meaningfully included in the more thoroughgoing response of bending not only the body, but the knees and head as well. Completely stopping before a red light may be said to include (since it "goes farther than") slowing slightly, or slowing considerably. We have here a principle of teleological inclusion which is the foundation of our telic continuum. It, is also apparent that such degrees of teleologically included behavior could not be recognized and selected were it not for the purpose for which the rule was established ; for that purpose establishes the criterion
(160) of their relevancy to the rule. We do not, for example, mistake such bendings of the body as are necessary in order to pick up a hat or a hymn-book with the bowings in prayer which are to be recorded as degrees of adherence to the devotional requirements. We must have the purpose or meaning of the entire situation before these partial steps can be identified.
Returning now to the requirement of a fairly general conformity in full compliance with the rule, the following question must be answered : What proportion must fully conform before we can have a societal situation to which our hypothesis of the J-curve of distribution can be applied? This question cannot be answered satisfactorily except by further experiment. For the purpose of our present hypothesis, however, we may say that the lower limit of this proportion of conformity must be approximately 50 per cent. Upon inspecting the solid black figures of our charts it will be seen that, with a single exception, all are either true J-forms of distribution or close approximations of that form. In practically all of these typical distributions the proportion of cases falling on the extreme left-hand position is 50 per cent or more. One drops to 46.2 per cent. Some of them range as high as 85 and 90 per cent. In Figure 9a, however, which is the only distribution departing conspicuously from J-form, there are only 32 per cent of the cases upon the first, and most frequently represented, position.[12] It seems justifiable, therefore, to accept the 50-per-cent limit as our tentative criterion for requisite conformity.
(161)
Putting together these three requirements, we may define the conditions under which the J-curve hypothesis may be said to operate as the conception of "a field of conforming behavior." A field of conforming behavior may be said to exist when one-half or more than one-half of the individuals included are performing an act which, in the form in which they do it, has been "prescribed" or deemed proper according to some rule which has been formulated or implicitly recognized for accomplishing a definite purpose.
With these qualifications in mind, let us see what generalizations can be suggested from the data thus far obtained. It is admitted that our case sampling has sometimes been inadequate and the fields investigated are few. Our principle is therefore stated purely in terms of an hypothesis to be tested by further observation.
Our hypothesis, then, is this: If, in any field of conforming behavior (see definition given above) we apply a scale whose steps are variations of the behavior, ranging from the prescribed or "proper" act, which most completely fulfills the behavior's purpose (on the left) to that which gives it the least recognizable amount of fulfillment (upon the right), the following will occur:
a. More instances will fall upon the step at the extreme left than upon any other.
b. The successive steps from left to right will have a respectively diminishing number of instances.
c. The decline in the number of instances will decrease as we proceed by successive steps from left to right.
To state the hypothesis in another form: In a field of conforming behavior degrees of conformity are distributed upon their appropriate telic continuum in decreasingly diminishing proportions as one proceeds from the most widely practiced form of the act toward the greatest recognizable deviation from that form.
Or, more simply: In a field of conforming behavior, the distribution of degrees of conformity upon their appropriate telic continuum is in the form of a curve of positive acceleration.[13]
(162)
II. DISTRIBUTION UPON AN EMPIRICAL OR NON-TELIC CONTINUUM: THE DOUBLE J-CURVE
We are now ready to turn from the telic continuum to behaviors as measured upon an objective continuum whose degrees are established not by meaning or purpose, but by disinterested physical measurement. Here we shall be concerned not with whether, or in what degree, the behavior fulfills a purpose or obeys a rule, but merely with its distribution in terms of small units of space, time, rapidity, or other non-telic dimensions. A man from Mars, for example, who knew nothing of the meaning of a church service or factory employment, or what constitutes "on time," or "lateness," could readily stand at the entrance of a building with a watch and record the number of people entering in successive five-minute intervals, beginning at a time when there was nobody arriving, and ending at a time when again no one was arriving. The same man from Mars might record the degree of acceleration or deceleration of automobiles approaching a red light, though he knew nothing whatever about city government. Our data, in other words, can be conceived as distributed upon a basic continuum of an empirical sort, a continuum of which our telic form has been derived by a special condensation and reinterpretation.
Figure 5 A is an empirical distribution summarizing some of the data gathered by Mr. Dickens in his time-clock studies. The data presented are the same as those in Figure 5. The scale used, however, is different in that the units On the baseline are non-telic; that is, instead of being construed as "on time," or "Ist half-hour of lateness," etc., they represent merely successive ten-minute intervals, from the earliest record the observer could obtain (time of opening the factory), which was 6:30 A.M., up to the latest time punched on any of the cards, which was about 9:40 A.M.[14] The
(163) employees were not supposed to start work earlier than the time indicated by the solid vertical line, namely, 7:25 A.m.; but if they started later they were penalized by a deduction from their pay. This, of course, was the type of scale which Mr. Dickens used in actually gathering his data. The telic distribution in Figure 5 was constructed later by combining all the cases arriving by 7:25 A.M. as "on time," and combining the intervals following into successive half-hours of lateness. (Such data as we have so far obtained on non-telic or empirical continua are presented in the shaded figures in the middle columns of the charts.) It is to be noted that the actual mode of conformity in punching the clock is 10 minutes to the left of the "factory rule" time for starting work, because it was necessary for many of the men to be on hand about ten minutes early in order to get their clothes changed, their machines put in readiness, etc. The dotted vertical line therefore indicates more truly the "economic" mode of the conformity distribution.
Now the main fact to observe is that this distribution upon a purely empirical continuum has two slopes rather than one. Both of these slopes are steep, but unequally so, with the mode which separates them forming a peak asymetrically placed between the extremes of the scale.[15] The cases which were all lumped together in our telic distribution as merely on time are now spread out in successively diminishing proportions on the left of the actual empirical mode, similarly to the way the cases are spread out on the right. We have a distribution on steps of "earliness" corresponding to that on steps of "lateness." The result is that we really have two J-curves, placed back to back, with their modes coinciding in the single mode of the entire distribution.
Figure 6 A, also from Dickens, shows the original distribution of the data of Figure 6 upon an empirical continuum. These are piece-workers, however, and consequently being "early" is a factor
(164) of considerable economic importance to them. The watchman supplied the information that from a half-hour to an hour of "earliness" could well be used by this particular class of workers in changing their clothes, laying out their tools, and getting materials and machines ready for! operation,- so as, to: secure the! maximum output and the highest pay possible for the day's work. This undoubtedly explains the long interval between the actual mode at the dotted vertical line and the "factory rule" time (solid vertical line). The largest proportion of this class of employees will be seen to have punched the clock at the first possible moment. Here again, if the observer had arrived before the factory doors opened, he might have found some of the men coming still earlier and waiting outside. In this case the 6:30-6:40 column would not be quite so high; and some cases would be distributed still further to the left. As a matter of fact, the factory records did show one or two cases (not indicated on the graphs) punching the clock earlier than 6:30, when the factory doors were inadvertently opened before that time. It seems justified, therefore, to draw a hypothetical dotted line representing the J-curve on the left-hand side of the empirical continuum. If we do this, we shall again observe that recording behaviors in a field of conformity upon an empirical continuum gives an asymmetrical, double J-shaped distribution.
Figure 7 A (Miss Loeb's original empirical plotting of the data in Figure 7) shows the exact day on which city welfare employees signed up with the C.W.A. The telic positions of promptness are now successive steps of twenty-four hours' duration, and the full range of steps is given before the modal date as well as after it. Some of the employees, perhaps sensing that a change would have to be made in their registration, began to sign up a few days before the general order was given. Strictly speaking, there was neither rule nor conformity (though there was a purpose) until this announcement was made; nevertheless we find individuals registering upon earlier days, corresponding to the "ahead of time" arrivals at the factory. This fact again gives us a sharply pointed, unequally sloping distribution resembling the double-J-form.
For the distributions of religious ceremonials the non-telic situation is somewhat more difficult to ascertain. Since the units of behavior are not capable of quantitative denotation, but are differing patterns of acts which are given significance only through being
(165) placed on a telic continuum, it seems impossible for an empirical continuum to be introduced. Nevertheless, it is likely that a nontelic continuum of some sort can be projected. A continuum which suggests itself is that of the degree of some personality trait which may characterize individuals falling upon different telic positions. In one of Miss Zambrowsky's sets of observations there was recorded a type of behavior which seems to belong at the left of the step of full compliance with the rule. This position comprises those who, while crossing themselves in the holy-water sacramental, stood still and made visible movements of the mouth in saying the prescribed prayer. Since merely praying "inwardly" seems to be regarded as adequate fulfillment of this ritual from an ecclesiastical standpoint, we may consider those who make lip movements as doing slightly more than is required. Such behavior is comparable roughly, to the behavior of those who arrive ahead of the required time in factory employment. Now it seems possible to regard these visibly praying individuals as more "pious" (either in outer manner or in fact) than those who made no lip movements. And we might translate our telic continuum of compliance with a rule into a continuum of degrees of the personality trait of "piety." And on such a non-telic, "piety" continuum, these persons who made visible lip movements could be recorded upon the position at the extreme left (that is, as most pious), and one position to the left of the telic mode. In Figure 8 A, a different set of observations from that shown in Figure 8, we find that 11.5 per cent of the total number fall upon this position. If this interpretation is correct, the complete, non-telic distribution of this observance again suggests the asymmetrical, off-center, double-J-form.
Figure 12 A is a distribution of the time of arrival of church attendants at a Sunday service in terms of four-minute intervals beginning with the first arrival and ending with the last. The vertical line marks the position of the beginning of the service. This set of observations (recorded by Miss Lathers) constitutes a different, but comparable, series from those shown in Figure 12. Periods of lateness or earliness are treated simply as empirical time intervals, and the "on time" cases are shown in their empirical distribution to the left of the opening time of the service. The form of the distribution suggests that shown in Figure 5 A and again illustrates the asymmetrical, double-J-pattern.
(166)
Of the distribution of traffic behavior upon an empirical continuum we have as yet made no observations. Figures 1 A and 4 A are purely hypothetical illustrations. The red-light-stop situation might be studied on a physical measurement scale in terms of degrees of deceleration of automobiles, ranging from a deceleration so great as to produce a quick stop a considerable distance behind the sidewalk crossing to no deceleration at all (or even to an acceleration in exceptional cases). Another method might be to record the point on the street at which speed was first diminished. A hypothetical curve of this character is shown in Figure 1 A. For Figure 4 we have constructed Figure 4 A, again hypothetical in character, showing a theoretical distribution upon an empirical time continuum of those who have parked their cars for a shorter as well as a longer time than that allowed by law.
Although our data are thus far meager we may now formulate tentatively the second portion of our hypothesis. t This portion deals with the complete distributions of conforming behavior secured by scales which are other than telic in character, distributions, in other words, which are in terms not of degrees of compliance with a rule, but of a simple, objectively descriptive statement.
Our hypothesis is as follows: In any field of conforming behavior (see definition previously given) the distribution of measurable variations of that behavior upon a relevant, but empirical, or non-telic, continuum is in the form of a steep, uni-modal, double-J-curve (that is, a curve having positive acceleration of both slopes), in which the mode is likely to be off-center, and the slopes are likely to be asymmetrical. The distribution, in other terms, is "leptokurtic," and probably asymmetrical both in area and in range.
One who approaches this problem for the first time will be likely to dismiss these distributions with the statement that they are merely., normal probability curves which have been steepened and skewed. This, in the writer's opinion, is an unfortunate error. An ordinary skewed curve, which is a departure (owing to disturbing factors) from the normal, is, like the normal curve, negatively accelerated in approaching the mode. Our double-J--curves, on the other hand, are positively accelerated throughout the entire length of both up-
(167) -ward slopes. The common notion of skewing as a phenomenon due to a selective error of sampling, producing a distortion where the curve would otherwise be symmetrical, does not apply to these conformity distributions; we must develop a new statistical conception in its place.
A moment's consideration will show that this is true. There is no such thing, for example, as purely normal probability distribution in the times of the required arrival of individuals at appointed places, in their stopping-behavior before red lights, or in their participation in church rituals. Without any economic pressures, sanctions, or other conformity influences acting upon the individuals to make them do a particular thing, they would not do these things at all, or else they would do them purely by chance. Now in the latter case the distribution would depend upon simple probability (not the so-called, compound probability of the normal curve) ; and the curve resulting would not be bell-shaped, but flat. The distribution of behavior in relation to a rule is that of the steep, double-J-form, produced by pressures toward conformity, or it is nothing at all. Its mode is placed by these pressures at a particular point, and this point is not determined by the probability curve of individual differences, though it may in some cases be identical with it. Laws, customs, and institutions are, by their very nature, telically biased ways of behaving; and the conformity curve is leptokurtic and generally asymmetrical from the beginning. The only exception to the statement that the double-J-curve is independent in formation from the normal curve is the fact that personality trait differences (which of course do tend toward a normal distribution) are represented as one factor in the total empirical distribution of the double-J-curve. It is to be noted, however, that these personality differences are superimposed upon (or centered at) a mode established and artificially heightened by quite a different set of influences, namely, conforming pressures. If our samples thus far obtained are supported by later observations, no resampling from mixed populations and no elimination of "disturbing influences" (such as traffic lights, factory rules, rituals, etc.) will serve to reduce these pointed, asymmetrical, conformity distributions to the normal, bell-shaped curve. Such treatment can reduce them only to the flat curve of chance or to the absence of any regularity whatsoever.
We are dealing here not with a single set of factors underlying
(168) a curve of distribution, but rather with several sets. Leaving out of account the mode of conformity, the descending distributions on the two sides represent, in part at least, different selective and steepening influences. On the right slope there are at work the societal penalties which will be inflicted in case the individual does not go far enough in his behavior so that he conforms; while on the lefthand slope there is at work the biological penalty of the needless hardship of inconvenience one must suffer through going further than conformity requires.
III. SUGGESTED INTERPRETATIONS: A FOUR-FACTOR THEORY OF CONFORMITY DISTRIBUTIONS
Throughout the preceding discussion we have hinted at the factors which seem to be at work in producing the asymmetrical, double- J-distribution. Our remaining task is to render their interpretation more explicit. The analysis of conformity distributions into all their contributing elements may prove to be a long and involved task. Without placing any dogmatic limitation on the number of possible factors, we may say that there are probably at least four major types of influences at work. We may call these, respectively, the conformity-producing agencies, the common biological tendencies, the personality-trait distribution tendency, and simple chance. The first two, conformity-producing and biological influence, seem to determine the horizontal position of the mode on the x axis and tend to make the curve steep and narrow; the latter two, personality-trait distribution and chance, tend, in opposition, to lower the mode and make the curve more bell-shaped, or spread out. We shall, discuss these in order.
A. Conformity-Producing Agencies. By this term we mean any common influences such as conditioning, punishment, education, propaganda, social approval or disapproval, the use of legal, ecclesiastical, or other symbols, the invoking of traditions or customs, the appeal to "institutions," and the power of institutional controls and leaders, all of these agencies tending to make people conform to a common mode. The laws of social psychology might be included here, such as the attitude of conformity, social facilitation, impression of universality, and the like, which, though secondary rather than primary in their operation, act in the direction of making the mode
(169) higher. A perfect conformity distribution, if such could be found, would be in the shape of a straight, vertical line at the point of the approved practice. The degree to which the distribution does pile up at this point and the extent to which the point is pushed toward one side or the other are in part functions of the strength of the conformity-producing influences.
B. Common Biological Tendencies. By treating the biological tendencies separately from the conformity agencies we do not imply that the latter are apart from the realm of biological realities. Unquestionably, behind our common sanctions, institutional symbols, and training, there lie biological needs which are fulfilled through these agencies. We refer here, however, not to the biological activities fulfilled indirectly through these "societal" agencies, but to those operating in a more direct and primitive manner, that is, those ways in which every human organism reacts to its raw, physical environment, and would react even if no other human beings were present. Professor Giddings' example of a temperature so low as to produce an almost complete similarity of individuals' protective behaviors is a case in point. Under ordinary conditions, the amount of clothing worn, food consumed, water drunk, exercise enjoyed, sleep taken, or the speed of walking, talking, etc., would probably tend, in an unselected population, toward the normal probability curve of individual differences. But as conditions change, as a sharp common need or crisis arises (such, for example, as a famine or a forest fire), the strength of the biological factor increases relatively to that of the other factors, and we find a displacement of the mode in the direction of that act or that degree of action which will secure the minimum adjustment necessary for life.
The part played by common biological tendencies yin our conformity distributions does not usually involve such crises as these. In fact, one of the principal reasons for having public regulation is to prevent serious maladjustments and assure a steady satisfaction of wants in advance of their arising. The common biological influences which do operate in these regulated activities may perhaps be summed up under the concepts of inertia, economy of effort, or resistance to the thwarting which is inevitable, in some degree, under any scheme of public control. An example would be the natural aversion to getting out of bed early in the morning in order to be at work at a required time, or the effort required to kneel in prayer
(170) or to stop and perform a ceremony before entering church. The ideal in practice is to have the modes which would be produced by the biological and the conforming influences (if they acted separately) coincide. An attempt at such agreement is illustrated by the successive timing of boulevard signal lights so that a motorist, if once he gets "in step" with the lights, can drive for a considerable distance without slowing down or shifting gears.
In the curve of the time of arrival of employees at a factory, Figures 5 A and 6 A, we may picture the common biological tendency as operating against the conformity-producing agency. Inertia must be overcome in order to get out of bed and get to the factory. If this inertia were the sole factor operative in determining time of arrival, it would probably push the modal time continually further to the right, until it reached an hour when most workers found it practically no effort to be present. The pressure brought to bear by the factory managers, however, to have the work begin early, and the system of pay by the piece which bestows a reward upon being punctual, tend to hold the time of modal arrival constant, or even to push it toward the left in order to offset the effects of the tendency in the opposite direction. Consequently, the mode actually established is probably a compromise between these two influences. More exactly stated, it is the point at which an equilibrium between the biological and the conformity-producing tendencies is established. Similarly, the modal stopping behavior of motorists facing the red signal light is assured only by maintaining the conformity-producing agency (punishment) at greater strength than the physiological inertia which must be overcome in applying brakes and shifting gears. As soon as law enforcement lapses we find motorists going ahead without slowing down. The J-curve is then broken down, to be replaced by a distribution showing a mode of fairly uniform city driving spread out somewhat by normal personality differences.
It will be noted that where biological tendencies are standardized in their operation through conformity-producing agencies the combined action of these influences may considerably increase conformity. This happens with regard to the rhythms of sleeping, eating, recreation, going to work, etc. The natural tendency to perform these acts at intervals fairly uniform for all is greatly reinforced by customary influences which demand the concerted, standardized action necessary for 'a social organization'' based upon" division of labor.
(171) When many human needs are satisfied, however, as they are today, not through individual effort, but by centralized mass production depending upon conformity of action, other problems emerge. Increasing conformity in time of eating, and at the same time making the fuel for cooking depend not upon individual effort but upon a concerted economic system (further conformity) of which a power plant or gas main is one component, sharply increases the demand upon this production source at a particular time. This is the problem of the "peak load" familiar in many branches of public utilities.
C. Tendencies of Personality-Trait Distribution. The third of our list of factors affecting the conformity pattern is one which needs to lessen the steepness of the slope and to spread out the distribution. Just as common biological tendencies operate with conformity to make individuals react alike, so the natural variations of physique, temperament, and endowment which characterize individuals tend to make them react differently. And this latter tendency, though it may be restricted in its operation, cannot fail to exert some influence upon the distribution. It is well known that if an attribute of living organisms which is capable of being measured is chosen and measured in an unselected group, the resulting distribution is likely to take the form of a symmetrical, bell-shaped curve of compound probability, in which the median, the mode, and the mean coincide. We are not, of course, arguing that the normal probability curve is universal in nature. It may depend largely upon human purposes and human scales of measurement. Our only assumption here is that when our equal-unit scales are applied to 'biometric and psychological functions we can predict that such a distribution will be likely to result unless there is some selective factor in the sampling. In its establishment of the mean and mode through a balancing of factors occurring by chance combination upon either side, the curve of normal probability differs in origin from the double-J-curve of conformity. In the latter case the distribution is built up, from the start, about a mode which is not established by probabilities, but is by its very nature highly selected, unbalanced, and improbable in the usual course of events. For it is set at that point by the voluntary actions of individual human beings, acts which involve so much caprice that they follow no law and cannot successfully be predicted.
Now when some conformity or biologic crisis establishes the mode of behavior at a' certain point 'of 'the continuum, what happens to
(172) the varying potentialities of individuals which, when not over-ruled by stronger influences, express themselves as a normal probability curve? What probably occurs is that the median of this normal personality curve moves over and coincides with the mode set by the conformity-producing and biological tendencies; and the individual differences, tapering off toward its extremities, exhibit themselves, in so far as the biologic or conformity pressures will permit, as respective degrees of deviation from this mode. The ordinary or typical individuals will comply with the rule; the individuals possessing unusual degrees of the trait brought into play will tend to do "more than" or "less than" the rule requires according to their degree of personality deviation.[16] The greater number, who possess little or no difference in their traits from the average, will probably not noticeably deviate from the modal behavior. They will, for example, arrive at the factory at just about the time they are expected. Those, on the other hand, who tend to be "before-hand" on all occasions, or who tend always to be more cautious than the average, will be likely to come early; and their degree of earliness will be in the proportion in which they possess this trait of promptness or caution. Finally, those who are characteristically inclined to "take their own time" on all occasions, or to be reckless, will probably manifest that dilatoriness or recklessness by being tardy; and their frequency or degree of tardiness may be an evidence of the degree in which they possess these traits.
Apart from this theoretical analysis, we have actual evidence that, of those individuals whose reactions fall along the tail of the J in our distribution of lateness, some, at least, do not fall there altogether
(173) by chance. On the contrary they are those who have a fairly constant individual tendency toward tardinesss, at least in regard to arrival at their daily work. In the distribution of degrees of tardiness shown in Figures 5 A and 6 A, the investigator has analyzed the individual time-card records and has computed the median of each individual's reactions. It was found, in the data of Figure 6 A, that, of those time-clock reactions which were more than 5 minutes late according to the factory rule, over 80 per cent were contributed by individuals whose median time was also tardy (data not shown on the charts).
In the right-hand columns of the charts we have suggested the possible distribution of personality differences by normal probability curves shown in dotted lines. These curves are shown as "moved over," so that their mode coincides with the mode of the double-J-distribution (also shown in dotted lines). This double-J-distribution is shown as a hypothetical curve, 'or as an actual frequency polygon taken from the column diagram immediately to the left. This device illustrates roughly the fact that the individuals of typical personality characteristics are the ones who conform, and also the fact that the individuals who deviate in their personal traits are distributed in successively diminishing numbers on the side of "more than" or "less than" the customary behavior. This arrangement also shows that, while the slopes of these normal curves run roughly parallel with the sides of the conformity distribution, they seldom coincide with the latter. The degree of the discrepancy between them is a rough measure of the failure of the pattern of behavior established about the required Practice to give expression to the personality differences of the individuals concerned. Since the difference between the two distributions is largely one of steepness, this discrepancy may be measured roughly by the index of kurtosis of the conformity distribution.[17]
In Figure 1 B we may take the hypothetical units of time expressing rate of deceleration in driving, or the first point of slowing up, as indices of the degree of some personality trait, ranging, for example, from aggressiveness or ascendance on one extreme (those who do not slow up at all) to timidity or submission on the other
(174) (those who slow up very "early" or stop far behind the crossing). We may assume that if there were no other factor present besides these personality differences the distribution (as indicated by broken lines) would be that of a normal probability curve. On this point, fortunately, we have some evidence. Mr. Dickens observed the behavior of motorists approaching an intersection on which cross traffic was approaching but which was without stop signs or signals of any kind. In such an instance, since there is nothing to stop the drivers except the motorists coming at right angles, and since both motorists (being approximately the same distance from the corner) have an equal chance to go ahead, the factor which will determine whether the motorist observed will go ahead or reduce his speed, or how much he will reduce his speed, will probably be the amount of aggressiveness or timidity which he possesses in comparison with the other driver. It may perhaps be some other trait than aggressiveness, but the principle will remain the same. Now if this hypothesis is correct, since traits of this sort are normally distributed, we should expect to find a normal probability distribution in the behaviors of the motorists observed. And this, indeed, is what Mr. Dickens has found. Of the 208 motorists whose behavior was observed, 35, or 17 per cent, stopped completely; 77, or 37 per cent, checked their speed and proceeded very slowly; 71, or 34 per cent, slowed slightly; and 25, or 12 per cent, proceeded without diminution of speed. These proportions will be seen to describe roughly the normal curve.
Now when a boulevard stop sign is interposed, with police supervision and punishment for violations, we may expect the mode of the motorists' behavior to shift to compliance with the rule of stopping. The personality continuum then "moves over" and the median of the personality distribution coincides with this mode of conforming behavior. Aggressive drivers, on facing the stop sign, will now tend, in the degree of their aggressiveness, to slow down only partially or to go ahead without change of speed. These cases will fall on the right-hand slope of the double-J-distribution. The timid drivers will not only telically conform to the requirement of stopping, but may stop more quickly, or further behind the crossing, in proportion to their degree of timidity, and will thus form the slope or tail of the double J on the left-hand side.
The shaded area in Figure 3 B shows the behavior of pedestrians
( 175) facing a red light in a city without pedestrian traffic-law enforcement, that is, where personality differences of boldness and timidity are permitted to have full play. Forty per cent of the individuals, the mode, exercised a "moderate" caution in that, if they went against the red light, they took the trouble to look to the right and left. Smaller percentages fell on the steps of a complete stop before the red light (relatively cautious or timid persons) and going ahead without even looking (relatively bold or aggressive persons) respectively. The general shape of the normal curve of personality traits is again suggested. By superimposing this hypothetical personality distribution upon an actual distribution of pedestrians' behavior in a city with enforcement (a frequency polygon suggested by Figure 3) we can theoretically place the individuals upon the conformity distribution according to their personality traits and can estimate also the success or failure of the conformity pattern in giving full expression to their personality differences.
In Figure 7 B, since the official rule for registration was not really in existence until the order to sign up with the C. W. A. was given, the conformity pattern allowed a distinguishing expression of only one-half of the personal differences in punctuality, viz., those upon the procrastinating side. This is because the ascent of the doubleJ-curve on the left is so steep as to constitute practically a reversed L. In Figures 8 B, 10 B, 11 B, 12 B, and 13 B, we may postulate some such trait as "religiosity" of "piety" as affecting the distribution in the curve of conforming behavior. In 10 B, 11 B, and 13 B we find that the actual or hypothetical distribution upon which the personality continuum is superimposed is steep on the left-hand side. Its discrepancy from the slope of the personality distribution is therefore greater upon that side. In other words, the manner in which individuals behave in performing certain prescribed religious rituals seems to give a wider range of self-expression to the less pious than to the more pious individuals. There seems to be little or no opportunity to express a personal religious feeling which is deeper than the average by any ceremonial which will distinguish the participant from the average conforming church member.
The extent to which the normal personality distribution is departed from in conformity distributions has an obvious practical significance. Its measurement gives a quantitative approach to the maladjustment between human nature, with its biological and psy-
( 176) -chological differences of individuals, and our somewhat standardized and mechanized civilization. In a completely mechanized industry, for example, where machines are run at a constant speed, there would be almost a complete elimination of the expression of individual differences. That is, there would be a maximum kurtosis of the curve of conforming behavior. Those who naturally reacted more rapidly than the machines would be able to run the machines; but they would have their capacities for more rapid action denied expression. Those who reacted characteristically more slowly than the machines would not only be prevented from carrying out these slower reactions in the industry, but would be disqualified from the industry altogether. The conformity-producing factor is not the only one which may suppress the exhibition and use of individual differences. The same effect may arise from the influence of common biological tendencies; but this is the case, as a rule, only in crises when the physical environment so changes as to require an unusual similarity of behavior in order to exist. In the case of conformityproducing influences, however, we have such an increase in kurtosis not as a result of crises or catastrophes, but as a part of the ordinary routine of living.18
D. Chance. We come finally to the consideration of simple probability. Logically, perhaps, this element should come first, since it is a background, without tendency of any kind, upon which the positive influences already mentioned play their rôles. Similarly to the "compounding" of probabilities in the personality distribution, simple chance represents a distributing rather than a concentrating tendency. It does not, however, produce the same form of distribution. For in the probability operating in personality distributions the occurrences are concentrated in a modal fashion upon a certain
(177) category and are spread out in diminishing proportions to the right and left, while in simple chance they are distributed equally in all categories. The situation is illustrated by tossing pennies. There are two categories, heads and tails. If enough trials are made, there will be found to be an equal number of cases falling in each. Similarly, in so far as simple chance factors are present in the distributions of individuals along our empirical continuum, there will tend to result an equal number of cases upon each step. If such factors were the only ones present, the curve would be perfectly flat. Although we may neglect this chance distribution for practical purposes (since it occurs everywhere equally), its presence should nevertheless be noted. It may be represented, for example, in the occasional behavior of motorists before traffic signals. Some doctor hurrying upon an emergency case might have to disregard traffic signals in varying degrees wherever possible, according to chance factors in the flow of traffic which permitted him to do so. Or again, a motorist's brakes might slip in an unpredictable degree, or there might be ice in varying degrees of slipperiness upon the pavement. Occurrences of this type might happen to people of any degree of ascendance or submission, or under various degrees of conformity-producing or biological pressure. They will tend to lower the proportion on the position of full compliance with the rule, and may in some cases tend to flatten the distribution. If there were no pressure of any kind exerted to make people come to church at a certain time, there would be about an equal likelihood, other things being equal, for individuals to come at any moment, of the day. This assumes, of course, a hypothetical situation in which there are no institutionalized times for waking, sleeping, eating, working, etc. Evidence of the simple chance factor is probably shown in the left-hand portion of Figure 7 A. Here we see the distribution of city employees who registered with the C. W. A. before any announcement was made that they must do so, hence before there was any incentive toward compliance with a rule or any standard through which individual differences in promptness could be expressed. We find that this left-hand portion of the distribution is flat. About as many persons had effective reasons for registering upon one day as upon another.
We are now ready to synthesize our analysis of the factors operative in fields of conforming behavior. Our theory is that the double-
(178) J-curve of conforming behavior plotted upon an empirical continuum is a summation of four component distributions, produced, respectively, by conformity-making agencies, common biological tendencies, personality differences, and chance.
We may conceive the empirical scale units of the conformity distribution as capable of being reinterpreted in four different ways as the base lines, respectively, of these four component distributions. For example, the empirical continuum of time of factory arrival, with its successive five-minute intervals, can be converted, first, into a telic continuum, by combining its five-minute units into positions of "on time," and of increasing degrees of "lateness." Second, it can be employed as a biological continuum, by treating its units as indices of the degrees of energy required to overcome physiological inertias, or as the degrees of certain universal, organic drives. Third, it can be construed as indirectly measuring the degree of some trait in which individuals characteristically differ. That is, it may be used as a personality-trait continuum. And, fourth, its units may represent categories into which, other influences being equal, behavioral occurrences might fall by chance. Suppose now that these four tendencies (conforming, biological, personality, and chance) were to act alone, or could be theoretically isolated in their distributional effects. We might then plot the distributions produced by each in a separate graph. And since all four graphs would have the same empirical continuum as their base line, they could be mathematically combined. Such a theoretically combined distribution would then be that which we might expect to discover if we were to go out (as we did in the case of the figures in our charts) and record the actual behaviors of individuals.
We have as yet no mathematical equations for such curves, nor any formula for the equilibrium of the forces which determine their modes. As a simple preliminary statement, we may say, however, that if F stands for force, b for common biological tendency, c for conformity-producing tendency, and p for the tendency toward distribution in a normal curve of personality traits (and omitting the chance factor since it operates equally in respect to all these tendencies), then (1) the horizontal position of the mode of the combined distribution, that is, its place on the x axis, will be the point at which
Fb-Fc=0
( 179) where the biological and conformity-producing tendencies are working in 'the opposite direction, and it will be determined by the summation
Fb+Fc
where these tendencies are working in the same direction; and (2) the height of the mode, that is, the position of its apex on the vertical or y axis, will be determined by the point where
FP – (Fb+Fc)=0
In conclusion, we may illustrate our theory by reference to a similar distribution in nature, namely, that of the grains of sand in a sand dune. The shape of a dune results from the combining of a number of forces, in the same way that our curves of conforming behavior combine the distributions of the several tendencies we have described. This illustration, of course, is not intended as an analogy between societal formations and a sand dune, but simply as a statement of the operation of similarly combined principles. The form of a sand dune, seen in cross section, like the form of our conformity distributions, is asymmetrical. It has a gentle slope on the windward side, and a steeper slope on the leeward side. On the windward side there are two forces operating, namely, the wind, which acts in a horizontal direction, and gravitation, which acts in a vertical direction. Sand particles are blown up the windward slope, and, when they pass the crest, are sheltered from the wind and hence are acted on by gravitation alone. This process is similar to the situation where a conformity-producing tendency (comparable to the wind) is acting to make people come to church at a certain time, and there is also a resistance (comparable to gravitation) due to biological inertia. The latter factor tends to lower conformity because of the effort required for compliance with the rule. Now when we pass the crest (mode) of our curve toward the left, we find only individuals who are on time or ahead of time; that is, the tendency of biological inertia was not strong enough to make them be late, just as gravitation was not strong enough to keep certain sand grains from being blown over the top of the dune. Nevertheless, once they are on the leeward side, that is, "on time," the conformity producing tendency is no longer a factor in determining the position
( 180) of these individuals along the scale. Biological inertia acts alone in this capacity. In both cases the tendency is to make the distribution as steep as possible. Just as the sand grain takes the shortest line possible to the ground, so people tend not to come to church any earlier than they need to.
Now the crest of the dune is the point of equilibrium between these two forces, gravitation and wind. Particles which are just about to fall over the edge are equally acted upon by both forces, and this equilibrium determines the point of the crest. Similarly, the apex of our behavior distributions represents the point where the conformity-producing and the biological forces are equal. This point will mark the piling-up of the greatest number of cases, just as the dune's height is greatest at this point.[19]
But let us go a little further. If wind and gravitation were the only factors operative, and if the wind were strong enough, it would overcome gravitation and blow the sand up into a straight vertical plane. If gravitation were very strong in comparison with the force of the wind, the wind might not disturb the sand at all. In this case the sand would lie in a flat, horizontal plane. There is usually present, however, some obstruction, such as a boulder, which starts the process of dune building; some object, in other words, which will give a differential in the relative effect of wind and gravitation. On one side the obstruction helps the wind prevail over gravitation as a dune-building agency by providing an inclined plane upon which the sand may rest as it is being blown horizontally and upward. On the other side the obstruction helps gravitation to become the more characteristic influence in constructing the dune's profile by not only sheltering the sand particles on that side from the wind, but by providing again an inclined plane down which the particles can roll. Consequently we do not have (as a result of wind action and gravitation) either a vertical or a horizontal plane, but a doubly sloping mound resulting from a differential between the two forces produced by a third factor and expressing a compromise between them.
( 181)
The situation is similar with human beings who are acting under conformity-producing and biological influences. There is not a complete subservience either to the one influence or to the other, but a compromise between them owing to a differential which has been established. This differential arises from the tendencies of behavior characteristic of the individuals concerned. Personality differences are the materials already present, just as the boulder at the foundation of the sand dune is present before the dune is formed. On the right side, by providing individuals who by nature do not go "far enough," the personality curve aids the conformity-producing factor as the stronger tendency in building the diminishingly non-conforming part of the distribution. On the left side, by providing individuals who characteristically do more than is expected,: it not only makes the conformity-producing agency irrelevant upon that side, but works with the biological tendency in producing the diminishingly "more than conforming" part of the distribution. Hence the resulting total pattern is neither completely horizontal nor completely vertical, but tapers off on both sides in the same manner as the sand dune.
We thus see that distributions of behavior in conformity situations are similar in form to such natural objects as sand dunes, waves, and snow drifts, and for precisely the same reason. Regularities are found as truly in the field of human behavior as in the fields of physics or geology, so far as the components of action and their statistical summation are concerned. Our present hypothesis is directed toward a quantitative formulation of these components and an understanding of their operation according to a definite law.
REFERENCES
1. ALLPORT, F. H. Psychology in relation to social and political problems. Chapter VII of Psychology at work, ed. by P. S. Achilles. New York: McGraw-Hill, 1932. Pp. 199-252.
2. ————. Institutional behavior. Chapel Hill: Univ. N. Car. Press, 1933. (Essay I.)
3. KATZ, D., & ALLPORT, F. H. Student attitudes. Syracuse, N. Y.: Craftsman Press, 1931. (See esp. Chap. XX.)
4. SCHANCK, R. L. A study of a community and its group and institutions conceived of as behaviors of individuals. Psychol. Monog., 1932, 43, No. 195. Pp. vi+133.
(182)
5. ————. Description of a rural community, and its groups and institutions in terms of common and reciprocal habits of individuals. In Research in social psychology of rural life. Soc. Sci. Res. Coun. Bull., No. 17, 1933, 18-23.
6. THURSTONE, L. L. Attitudes can be measured. Amer. J. Sociol., 1928, 33, 529-554.
Syracuse University
Syracuse, New York
L'HYPOTHESE DE LA COURBE J DU COMPORTEMENT CONFORMANT
(Résumé)
En considérant la conformité du comportement humain, les étudiants de la société se sont intéressés généralement à la "norme", c'est-à-dire, à l'acte fait par la plupart des gens. Cet article appuie sur l'importance d'étudier la distribution entière, y compris les degrés de la conformité partielle, ainsi que ceux de la non-conformité. On recommande deux continua de mesure. Le premier est le continuum télique, sur lequel sont projetées les déviations de l'acte modal lesquelles expriment son but à des degrés variants. Un exemple est le degré de ralentissement des chauffeurs d'automobile en s'approchant d'un signal rouge d'arrêt, ou le degré de salutation des membres d'église en s'asseyant sur leurs bancs. Le second continuum est empirique, et est basé sur des unités objectives et physiques du temps, de l'espace, etc. Tout au contraire du continuum télique, il permet la distribution séparée de ces cas de ceux qui "font plus que de conformer." Un "champ de comportement conformant" est défini comme une situation oÿ la moitié (ou plus) des individus font l'acte qui satisfait une règle établie pour remplir un but défini. On a noté les comportements des individus en treize situations; institutionnelles ou de; conformité (politiques, économiques, et religieuses).
On suggère les généralisations suivantes: (a) Dans un champ de comportement conformant, les variations du rendement, quand on les exprime sur leur continuum télique approprié variant d'une conformité complète à la règle à une déviation reconnaissable maximum, sont en forme d'une courbe d'accélération positive. (b) Dans un champ de comportement conformant, les variations du rendement, quand on les exprime sur un continuum empirique, sont en forme d'une courbe raide, non modale, double J, laquelle est ordinairement asymmétrique en aire et portée.
En interprétant les distributions de la conformité,-on a reconnu quatre influences composantes: Les tendances qui produisent la conformité (institutionalisantes), les tendances ordinaires biologiques, les tendances à la distribution normale des traits de personnalité, et le hasard. Les deux premières rendent plus raide la distribution à la mode, et déterminent la position modale. Elles sont opposées par les deux dernières influences, que tendant à baisser la mode et à étendre la distribution, expliquant ainsi la "queue" du J. On suggère, comme illustration, que ces influences travaillent ensemble pour produire la distribution empirique de conformité, à peu près comme les "forces de la nature" se combinent pour construire une dune de sable.
ALLPORT
(183)
DIE J-KURVE-HYPOTHESE DES GLEICHFÖRMIGEN VERHALTENS
(Referat)
Hinsichtlich des gleichförmigen menschlichen Verhaltens haben sich die Soziologen im allgemeinen für die Norm interessiert, d. h. für den Akt, den die meisten Leute ausführen. Dieser Artikel legt viel Wert auf die Untersuchung der ganzen Verteilung, die auch Grade von Teilgleichförmigkeit oder Ungleichförmigkeit enthält. Zwei messbare Kontinua werden empfohlen. Das erste ist das teleologische Kontinuum, auf das die Abweichungen von dem modalen Akt, der seinen Zweck in verschiedenen Graden äussert, projektiert werden. Ein Beispiel davon ist der Grad des Bremsens von den Autofahrern beim roten Verkehrslicht, oder der Grad der Verbeugung der Kirchgänger beim Sichsetzen. Das zweite is ein empirisches Kontinuum, und beruht auf objektiven, physikalischen Einheiten von Zeit, Raum, usw. Ungleich dem teleologischen Kontinuum gestattet es die getrennte Verteilung von denjenigen Fällen, die "mehr als gleichförmig" sind. Ein "Feld von gleichförmigem Verhalten" wird als eine Situation bezeichnet, wo die Hälfte (oder mehr) der Individuen den Akt ausführen, der einer Regel zur Vollziehung eines bestimmten Zweckes folgt. Die Verhaltungsweisen von Individuen in dreizehn Gleichförmigkeitssituationen (politischen, ökonomischen, religiösen) wurden untersucht.
Die folgenden Verallgemeinerungen dürfen aufgestellt werden: (a) In einem Feld von gleichförmigem Verhalten nehmen die Variationen im Verhalten, wenn sie in eine passende teleologische Verteilung von vollkommener Gleichförmigkeit mit der Regel bis zu einer erkennbaren Maximalabweichung gebracht werden, die Form einer Kurve von positiver Beschleunigung an. (b) In einem Feld von gleichförmigen Verhalten nehmen die Variationen im Verhalten, wenn sie in eine empirische Verteilung gebracht werden, die Form einer steilen, unmodalen "Doppel-J-Kurve" an, die gewöhnlich asymmetrisch an Flächeninhalt und Umfang ist.
Bei der Deutung der gleichförmigen Verteilungen sind vier zusammengesetzte Einflüsse erkannt worden: gleichförmigkeitserzeugende Tendenzen, allgemeine biologische Tendenzen, Tendenzen nach einer normalen Persönlichkeitsverteilung, und Zufall.' Die beiden ersten machen die Verteilung bei dem grössten Häufigkeitswert steil und bestimmen die modale Stellung. Sie stehen den zwei letzten gegenüber, welche den grössten Häufigkeitswert niedrig zu machen und die Verteilung auszubreiten neigen, wodurch der "Schwanz" des J erklärt wird. Es wird vorgeschlagen, dass diese Einflüsse zusammenwirken, um die empirische gleichförmige Verteilung zu erzeugen, ganz wie die "Naturkräfte" sich zusammensetzen, um die Dünnen zu bauen.
ALLPORT